
Uncoiling the spiral: Maths and hallucinations
Think drug-induced hallucinations, and the whirly, spirally, tunnel-vision-like patterns of psychedelic imagery immediately spring to mind. But it's not just hallucinogenic drugs like LSD, cannabis or mescaline that conjure up these geometric structures. People have reported seeing them in near-death experiences, as a result of disorders like epilepsy and schizophrenia, following sensory deprivation, or even just after applying pressure to the eyeballs. So common are these geometric hallucinations, that in the last century scientists began asking themselves if they couldn't tell us something fundamental about how our brains are wired up. And it seems that they can.
![Computer generated representations of form constants. The top two images represent a funnel and a spiral as seen after taking LSD, the bottom left image is a honeycomb generated by marijuana, and the bottom right image is a cobweb. Image from <a href='#one'>[1]</a>, used by permission.](/issue53/features/hallucinations/simulation.jpg)
Computer generated representations of form constants. The top two images represent a funnel and a spiral as seen after taking LSD, the bottom left image is a honeycomb generated by marijuana, and the bottom right image is a cobweb. Image from [1], used by permission.
Geometric hallucinations were first studied systematically in the 1920s by the German-American psychologist Heinrich Klüver. Klüver's interest in visual perception had led him to experiment with peyote, that cactus made famous by Carlos Castaneda, whose psychoactive ingredient mescaline played an important role in the shamanistic rituals of many central American tribes. Mescaline was well-known for inducing striking visual hallucinations. Popping peyote buttons with his assistant in the laboratory, Klüver noticed the repeating geometric shapes in mescaline-induced hallucinations and classified them into four types, which he called form constants: tunnels and funnels, spirals, lattices including honeycombs and triangles, and cobwebs.
In the 1970s the mathematicians Jack D. Cowan and G. Bard Ermentrout used Klüver's classification to build a theory describing what is going on in our brain when it tricks us into believing that we are seeing geometric patterns. Their theory has since been elaborated by other scientists, including Paul Bressloff, Professor of Mathematical and Computational Neuroscience at the newly established Oxford Centre for Collaborative Applied Mathematics.
How the cortex got its stripes...
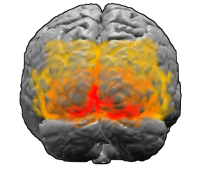
The visual cortex: the area V1 is shown in red. Image: Washington irving
In humans and mammals the first area of the visual cortex to process visual information is known as V1. Experimental evidence, for example from fMRI scans, suggests that Klüver's patterns, too, originate largely in V1, rather than later on in the visual system. Like the rest of the brain, V1 has a complex, crinkly, folded-up structure, but there's a surprisingly straight-forward way of translating what we see in our visual field to neural activity in V1. "If you imagine unfolding [V1]," says Bressloff, "You can think of it as neural tissue a few millimetres thick with various layers of neurons. To a first approximation, the neurons through the depth of the cortex behave in a similar way, so if you compress those neurons together, you can think of V1 as a two-dimensional sheet."
From the visual field to the visual cortex
Think of the visual field as a flat sheet, endowed with polar coordinates: each point $P$ in the field is defined by two numbers $(r, \theta)$, where $r$ is its distance to the origin $O$, and $\theta$ the angle between the line $OP$ and the $x$-axis. The origin corresponds to the centre of the visual field. V1 is also modelled as a flat sheet, this time endowed with the usual Cartesian coordinates $(x,y)$. The exact coordinate map between the visual field and the flat model of V1 is complicated to write down, but for points in the visual field that are away from the centre of the field (so for $r$ sufficiently large) it is similar to the logarithmic map $$x=\ln{r} \;\;\;\;\;\;\;\; y= \theta.$$ This map transforms a circle of radius $r$ in the visual field into a vertical straight line segment at $x=\ln{r}$, and a ray emanating from the origin $O$ at angle $\theta$ into a horizontal straight line segment at $y=\theta$.
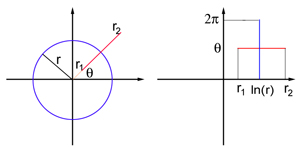
An object or scene in the visual world is projected as a two-dimensional image on the retina of each eye, so what we see can also be treated as flat sheet: the visual field. Every point on this sheet can be pin-pointed by two coordinates, just like a point on a map, or a point on the flat model of V1. The alternating regions of light and dark that make up a geometric hallucination are caused by alternating regions of high and low neural activity in V1 — regions where the neurons are firing very rapidly and regions where they are not firing rapidly.
To translate visual patterns to neural activity, what is needed is a coordinate map, a rule which links each point in the visual field to a point on the flat model of V1. In the 1970s scientists including Cowan came up with just such a map, based on anatomical knowledge of how neurons in the retina communicate with neurons in V1 (see the box on the right for more detail). For each light or dark region in the visual field, the map identifies a region of high or low neural activity in V1.
So how does this retino-cortical map transform Klüver's geometric patterns? It turns out that hallucinations comprising spirals, circles, and rays that emanate from the centre correspond to stripes of neural activity in V1 that are inclined at given angles. Lattices like honeycombs or chequer-boards correspond to hexagonal activity patterns in V1. This in itself might not have appeared particularly exciting, but there was a precedent: stripes and hexagons are exactly what scientists had seen when modelling other instances of pattern formation, for example convection in fluids, or, more strikingly, the emergence of spots and stripes in animal coats. The mathematics that drives this pattern formation was well known, and it now suggested a mechanism for modelling the workings of the visual cortex too.
...and how the leopard got its spots
The first model of pattern formation in animal coats goes back to Alan Turing, better known as the father of modern computer science and Bletchley Park code breaker. Turing was interested in how a spatially homogeneous system, such as a uniform ball of cells making up an animal embryo, can generate a spatially inhomogeneous but static pattern, such as the stripes of a zebra.
Animal pattern equations
For the sake of simplicity, imagine the embryo as a one-dimensional line. At any time $t$ and any point $x$ on the embryo, the concentrations of the activator and inhibitor are given by the functions $A(x,t)$ and $I(x,t)$ respectively. These functions vary over time according to the following rules:
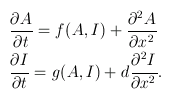
The first term on the right-hand side of each equation describes how much activator/inhibitor is being produced. These terms are functions of activator and inhibitor concentrations because they both affect the reaction rate.
The second term in each equation is a second derivative describing how quickly the gradient of activator/inhibitor is changing. These terms give the rate of diffusion.
The extra term, d, on the right-hand side of the second equation is the diffusion coefficient — how much quicker the inhibitor diffuses than the activator. The inhibitor being a faster diffuser was shown by Turing to be pivotal in driving the process of pattern generation.
Turing hypothesised that these animal patterns are a result of a reaction-diffusion process. Imagine an animal embryo which has two chemicals living in its skin. One of the two chemicals is an inhibitor, which suppresses the production of both itself and the other chemical. The other, an activator, promotes the production of both.
Initially, at time zero in Turing's model, the two chemicals exactly balance each other — they are in equilibrium, and their concentrations at the various points on the embryo do not change over time. But now imagine that, for some reason or other, the concentration of activator increases slightly at one point. This small perturbation sets the system into action. The higher local concentration of activator means that more activator and inhibitor are produced there — this is a reaction. But both chemicals also diffuse through the embryo skin, inhibiting or activating production elsewhere.
For example, if the inhibitor diffuses faster than the activator, then it quickly spreads around the point of perturbation and decreases the concentration of activator there. So you end up with a region of high activator concentration bordered by high inhibitor concentration — in other words, you have a spot of activator on a background of inhibitor. Depending on the rates at which the two chemicals diffuse, it is possible that such a spotty pattern arises all over the skin of the embryo, and eventually stabilises. If the activator also promotes the generation of a pigment in the skin of the animal, then this pattern can be made visible. (See the Plus article How the leopard got its spots for more detail.)
Turing wrote down a set of differential equations which describe the competition between the two chemicals (see the box on the right), and which you can let evolve over time, to see if any patterns emerge. The equations depend on parameters capturing the rate at which the two chemicals diffuse: if you choose them correctly, the system will eventually stabilise on a particular pattern, and you can vary the pattern by varying the parameters. Here is an applet (kindly provided by Chris Jennings) which allows you to play with different parameters and see the patterns form.
Patterns in the brain
Neural activity in the brain isn't a reaction-diffusion process, but there are analogies to Turing's model. "Neurons send signals to each other via their output lines called axons," says Bressloff. Neurons respond to each other's signals, so we have a reaction. "[The signals] propagate so quickly relative to the process of pattern formation, that you can think of them as instantaneous interactions." So rather than diffusion, which is a local process, we have instantaneous interaction at a distance in this case. The roles of activator and inhibitor are played by two different classes of neurons. "There are neurons which are excitatory — they make other neurons more likely to become active — and there are inhibitory neurons, which make other neurons less likely to become active," says Bressloff. "The competition between the two classes of neurons is the analogue of the activator-inhibitor mechanism in Turing's model."
![Stripy, hexagonal and square patterns of neural activity in V1 generated by a mathematical model. Image from <a href='#one'>[1]</a>, used by permission.](/issue53/features/hallucinations/v1pattern.jpg)
Stripy, hexagonal and square patterns of neural activity in V1 generated by a mathematical model. Image from [1], used by permission.
Inspired by the analogies to Turing's process, Cowan and Ermentrout constructed a model of neural activity in V1, using a set of equations that had been formulated by Cowan and Hugh Wilson. Although the equations are more complicated than Turing's, you can still play the same game, letting the system evolve over time and see if patterns in neural activity evolve. "You find that, under certain circumstances, if you turn up a parameter which represents, for example, the effect of a drug on the cortex, then this leads to a growth of periodic patterns," says Bressloff.
Cowan and Ermentrout's model suggests that geometric hallucinations are a result of an instability in V1: something, for example the presence of a drug, throws the neural network off its equilibrium, kicking into action a snowballing interaction between excitatory and inhibitory neurons, which then stabilises in a stripy or hexagonal pattern of neural activity in V1. In the visual field we then "see" this pattern in the shape of the geometric structures described by Klüver.
Symmetries in the brain
In reality, things aren't quite as simple as in Cowan and Ermentrout's model, because neurons don't only respond to light and dark images. Through the thickness of V1, neurons are arranged in collections of columns, known as hypercolumns, with each hypercolumn roughly responding to a small region of the visual field. But the neurons in a hypercolumn aren't all the same: apart from detecting light and dark regions, each neuron specialises in detecting local edges — the separation lines between light and dark regions in a part of an image — of a particular orientation. Some detect horizontal edges, others detect vertical edges, others edges that are inclined at a 45° angle, and so on. Each hypercolumn contains columns of neurons of all orientation preferences, so that a hypercolumn can respond to edges of all orientations from a particular region of the visual field. It is the lay-out of hypercolumns and orientation preferences that enables us to detect contours, surfaces and textures in the visual world.
![Connections in V1: Neurons interact with most other neurons within a hypercolumn. But they only interact with neurons in other hypercolumns, if the columns lie in the direction of their orientation, and if the neurons have the same preference. Image from <a href='#two'>[2]</a>, used by permission.](/issue53/features/hallucinations/connections.jpg)
Connections in V1: Neurons interact with most other neurons within a hypercolumn. But they only interact with neurons in other hypercolumns, if the columns lie in the direction of their orientation, and if the neurons have the same preference. Image from [2], used by permission.
Over recent years, much anatomical evidence has accumulated showing just how neurons with various orientation preferences interact. Within their own hypercolumn, neurons tend to interact with most other neurons, regardless of their orientation preference. But when it comes to neurons in other hypercolumns they are more selective, only interacting with those of similar orientations and in a way which ensures that we can detect continuous contours in the visual world.
Bressloff, in collaboration with Cowan, the mathematician Martin Golubitsky and others, has generalised Cowan and Ermentrout's original model to take account of this new anatomical evidence. They again used the plane as the basis for a model of V1: each hypercolumn is represented by a point $(x,y)$ on the plane, while each point $(x,y)$ in turn corresponds to a hypercolumn. Neurons with a given orientation preference $\theta$ (where $\theta$ is an angle between 0 and $\pi$) are represented by the location $(x,y)$ of the hypercolumn they're in, together with the angle $\theta$, that is, they are represented by three bits of information, $(x,y,\theta)$. So in this model V1 is not just a plane, but a plane together with a full set of orientations for each point.
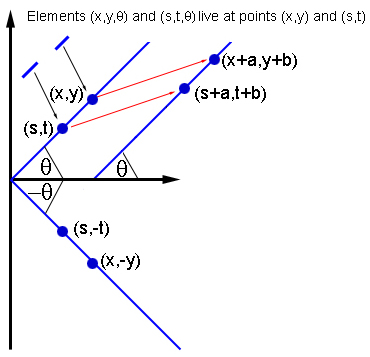
If two elements (x,y,θ) and (s,t,θ) interact, then so do the elements of the same orientation at (x+a,y+b) and (s+a,t+b), and the elements of orientation -θ at (x,-y) and (s,-t).
In keeping with anatomical evidence, Bressloff and his colleagues assumed that a neuron represented by $(x_0,y_0,\theta_0)$ interacts with all other neurons in the same hypercolumn $(x_0,y_0).$ But it only interacts with neurons in other hypercolumns, if these hypercolumns lie in their preferred direction $\theta_0$: on the plane, draw a line through $(x_0,y_0)$ of inclination $\theta_0.$ Then the neurons represented by $(x_0,y_0,\theta_0)$ interact only with neurons in hypercolumns that lie on this line, and which have the same preferred orientation $\theta_0$.
This interaction pattern is highly symmetric. For example, the pattern doesn't appear any different if you shift the plane along in a given direction by a given distance: if two elements $(x_0,y_0,\theta_0)$ and $(s_0,t_0,\phi_0)$ interact, then the elements you get to by shifting along, that is $(x_0+a,y_0+b,\theta_0)$ and $(s_0+a,t_0+b,\phi_0)$ for some $a$ and $b$, interact in the same way. In a similar way, the pattern is also invariant under rotations and reflections of the plane.
![A lattice tunnel hallucination generated by the mathematical model. It strongly resembles hallucinations seen after taking marijuana. Image from <a href='#one'>[1]</a>, used by permission.](/issue53/features/hallucinations/new.jpg)
A lattice tunnel hallucination generated by the mathematical model. It strongly resembles hallucinations seen after taking marijuana. Image from [1], used by permission.
Bressloff and his colleagues used a generalised version of the equations from the original model to let the system evolve. The result was a model that is not only more accurate in terms of the anatomy of V1, but can also generate geometric patterns in the visual field that the original model was unable to produce. These include lattice tunnels, honeycombs and cobwebs that are better characterised in terms of the orientation of contours within them, than in terms of contrasting regions of light and dark.
What's more, the model is sensitive to the symmetries in the interaction patterns between neurons: the mathematics shows that it is these symmetries that drive the formation of periodic patterns of neural activity. So the model suggests that it is the lay-out of hypercolumns and orientation preferences, in other words the mechanisms that enable us to detect edges, contours, surfaces and textures in the visual world, that generate the hallucinations. It is when these mechanism become unstable, for example due to the influence of a drug, that patterns of neural activity arise, which in turn translate to the visual hallucinations.
Beyond hallucinations
Bressloff's model does not only provide insight into the mechanisms that drive visual hallucinations, but also gives clues about brain architecture in a wider sense. In collaboration with his wife, an experimental neuroscientist, Bressloff has looked at the connection circuits between hypercolumns in normal vision, to see how visual images are processed. "People used to think that neurons in V1 just detect local edges, and that you have to go to higher levels in the brain to put these edges together to detect more complicated features like contours and surfaces. But the work I have done with my wife shows that these structures in V1 actually allow the earlier visual cortex to detect contours and do more global processing. It used to be thought that you process more and more complex aspects of an image as you go higher up in the brain. But now it's realised that there is a huge amount of feedback between higher and lower cortical areas. It's not a simple hierarchical process, but an incredibly complicated and active system it will take many years to understand."
Practical applications of this work include computer vision — computer scientists are already building the inter-connectivity structures that Bressloff and his colleagues played around with into their models, with the aim of teaching computers to detect contours and textures. On a more speculative note, Bressloff's research may also one day help to restore vision to visually impaired people. "The question here is if you can somehow stimulate part of the visual cortex, [bypassing the eye], and use that to guide a blind person," says Bressloff. "If one can understand how the cortex is wired up and responds to stimulation, perhaps one would then have a better way of stimulating it in the right way."
There are even applications that have nothing at all to do with the brain. Bressloff applied the insights from this work to other situations in which objects are located in space and also have an orientation, for example fibroblast cells found in human and animal tissue. He showed that under certain circumstances these interacting cells and molecules can line up and form patterns analogous to those that arise in V1.
People have reported seeing visual hallucinations since the dawn of time and in almost all human cultures — hallucinatory images have even been found in petroglyphs and cave paintings. In shamanistic traditions around the world they have been regarded as messages from the spirit world. Few neuroscientists today would agree that spirits have anything to do with it, but as messengers from a hidden world — this time the hidden world of our brain — these hallucinations seem to have lost none of their potency.
Further reading
Bressloff's work on visual hallucinations is summarised in the paper What geometric visual hallucinations tell us about the visual cortex ([1]). A more detailed description can be found in the paper Geometric visual hallucinations, Euclidean symmetry and the functional architecture of striate cortex ([2]).
About this article

Paul Bressloff was interviewed by Marianne Freiberger, co-editor of Plus, in August 2009.
Paul Bressloff graduated with a degree in physics from Oxford 1981 and completed a PhD in string theory at King's College London in 1988. He then spent five years as a research Scientist at GEC-Marconi Hirst Research Centre, where he worked on dynamical systems theory and neural networks. In 1993 he joined the Department of Mathematical Sciences at Loughborough University, where he built up a group in mathematical biology and became Professor of Applied Mathematics in 1998. Tenured Full Professor at the University of Utah he built up a group in mathematical neuroscience between 2001 and 2009. He returned to the UK in July 2009 to take up an appointment as a University Research Professor in Mathematical Neuroscience at the University of Oxford. He has also been awarded a Royal Society Wolfson Merit Award (2009-2014).
Bressloff has spent the past 20 years working at the multidisciplinary interface between applied mathematics, theoretical physics and neuroscience. The main focus of his work is to understand how the brain functions as a complex dynamical system at multiple spatial and temporal scales in healthy and diseased brains. He has published more than 120 papers in research journals and co-authored one book. He has mentored ten PhD students and four postdocs.
Comments
Anonymous
Ummm, I don't know anyone who's ever hallucinated after "taking" marujana (you smoke it, by the way). Not quite sure what kind of "research" went into that.
Interesting article nonetheless.
Anonymous
I have. It wasn't good. You can eat it, smoke it and drink it.
Anonymous
Yes it is possible to hallucinate with marujana, it's more common through ingestion but also possible via inhalation in extreme doses. I have done both & the latter was much more pleasant than the former, but I imagine it's different every time & also dependent on what strain of marujana you are using.
Anonymous
As a student of Psychology at University of Massachusetts, I was once assigned a research project on altered states of consciousness. Having already experienced pscilocybin mushrooms 60 separate times, as well as LSD, MDMA, MDA, and Salvia on a few occasions, I was excited to be able to discuss such a topic in purely objective terms.
First, you can absolutely hallucinate off marijuana. Marijuana itself is a mild hallucinogen and smoking an extreme amount will induce hallucinations.
There are 3 categories of Hallucinogens.
1-Psychedelics.
Mushrooms, marijuana, and LSD all fall under this category. The human brain has a filtering system for perception, allowing us to perceive only a limited amount of the onformation received by our senses. Psychedelics essentially turn off this filter, flooding our brains with sensory information. Seeing as our brains are constantly working to organize sensory information to construct our perceived reality, the increase in information requires the brain to organize more data. This results in an altered state of consciousness.
Interesting to note is that pscilocybin (mushrooms) has a molecular structure very similar to the neurotransmitter serotonin and essentially acts as a neurotransmitter upon ingestion. It actually binds to serotonin and alters the information carried on the neurotransmitter, effectively hijacking the serotonin.
2-Dissociatives
Salvia best represents the effects of these hallucinogens. The brain experiences sensory deprivation and sensory separation, leading the brain to essentially "fill in the blanks" when it comes to information relating to perception of reality. There are ways of inducing sensory deprivation without the use of drugs, such as meditation, sensory deprivation tanks, and lucid dreaming.
3- Deliriants
Datira seeds and other deliriants shut off your acetylcholine neurotransmitter which is known to work in relation to memory, as Alzheimers parients all show a significant depletion of acetylcholine. Trip reports are never good, for the effects it has on this vital neurotransmitter can lead to one perceiving their mirror reflection as a stranger.
DMT is hard to categorize because it is all pervasive in its effects. It works as a psychedelic and a dissociate. Its chemical structure is also of extreme similarity to that of serotonin and pscilocybin. Due to it existing within the brain, DMT is theorized by some to be a neurotransmitter that remains inactive, firing only at birth and death. However, DMT's specific function is still a mystery and no clear explanation can be given on its profound hallucinations
Anonymous
Hi - I really liked reading your post as you combined three elements that made you interesting for me to read; your personnel experience with these substances, your scientific knowledge and your enjoyable to read writing style where your passion for the subject matter was felt by me.
I would think you would make a terrific contributor to a publication like MAPS (multidisciplinary association of psychedelic studies) puts out quarterly.
I am interested in the data that shows release of naturally occurring dmt at birth and death. I can understand from reports of near death experiences that this could correlate with the experiences of people taking dmt but when one is born why would dmt be naturally released at this time and what is the evidence for this?
Chris Urgeleit
Anonymous
There is a book about it called DMT The Spirit Molecule, by Rick Strassman.
Anonymous
I actually have after taking Marijuana. Always tried to tell my friends about it, never could find a way to describe it though. Until one day in psychology they mentioned lattice shape hallucinations.
Nick
When I was young I had that outlook.. But the way we experience drugs is very subjective. The things we have experienced, what we believe, our position in life relative to others, drastically affects our drug experiences. I have noticed that with aging, my experiences with marijuana have changed and now I understand them to be more hallucinatory. Do not think that your experience is the only experience!
Anonymous
Sorry to tell you that you are dead wrong. The geometric patterns are part of what makes up our reality. Lsd, dmt, and peyote hust make it so we can view them.
Anonymous
You're certainly welcome to think that, but you're only deluding yourself.
Anonymous
The part you're both missing is that the universe is expansive enough to contain both perspectives equally
Anonymous
You're comment has a very metaphysical basis. There's no empirical evidence suggesting that LSD, DMT, and Peyote equip us with the ability to see more of our "reality". It's all conjecture that has never been proven. The fact that you take it on faith worries me. You aren't a scientist, are you? A scientist would never treat a conjecture as indisputable fact. YOU SIR, are wrong.
Anonymous
And you seem to be speaking in an equally strong absolute...
Anonymous
but minus the argumentum ad ignorantiam.
Anonymous
Have you seen the study where they slowly degrade the quality of letters until a passage becomes illegible? The group on psilocybin is consistently able to derive the correct meaning from the text at levels the control group cannot.
Pupil dilation, literally allows more light to enter the eye and more signal to travel down the optical nerve.
In fact, serotonin (the primary neurotransmitter stimulated by most psychedelics) is heavily involved in perception and the internal processes by which we make up our realities.
Like, no, this doesn't prove any of the things people have extrapolated it into, but maybe think twice before saying there is no evidence to even suggest such a thing.
Anon
I’m glad to see someone is actually correcting them! That’s because instead of the information going thru the thalamus filter (which prevent information overload) to the region called the posterior cingulate cortex. So you regularly dont see reality as it is because it would be too much for you to handle. Thats the whole point of the thalamus filter. Im not sure why the person above was belittling someone because “tHeY aReNt A sCiEnTiSt” but since the posterior cingulate cortex is thought to play a role in the shaping of ones self, the information overload is probably a factor in ego death. So what you see on acid could really be closer to what “reality” is.
Ricardo
In my younger days I got stoned after drinking. I was unable to walk for a while. Later I closed my eyes and saw the most complex pattern I had ever seen. I thought it was the network of the human brain- well mine. For a while, everything made sense- life, the Universe - everything - then I think I probably walked or cycled home...
Anonymous
You don't "hallucinate" on LSD, your perception is altered along with possible cognitive shifts. You don't "take" marijuana, you smoke it (or eat if it's been made into an edible).
Anonymous
So LSD visuals aren't hallucinations? Ha.
And I don't see what's wrong with the word "take". No meaning is lost there, and it's a trivial difference to quibble over.
Anonymous
I smoke a lot of marijuana but I never hallucinated - Sometimes I fell like Im levitating If Im laying in my bed.I dont see spirals or geometric forms...
On LSD I see some people changing form or shape and the kaleidoscopes everywhere,...And the colours are more vivid. If I close my eyes the kaleidoscopes and fractals are more intense and sometimes fluorescent. I trip more with my eyes closed even when the light Is strong.
On peyote and san Pedro I didnt see the fractals and geometric forms but everything was fluid and soft - like Im inside an living organism that moves with me and around me. It was more the psychological feeling than visual.
Anonymous
Geometrical hallucinations are just one type of visual hallucinations. Under certain circumstances one may "see" complicated objects such as faces, people, house, landscapes, etc. in visual hallucinations. How can this kind of research generalize from geometrical hallucinations to these more complicated ones?
Anonymous
Just to hazard a guess, one could assume it has something to do with the way our brain categorizes different "contours" and patterns in the visual fields as being faces or fingers or really anything more than just lines. Take looking at a cloud, and seeing a vague shape of a face and recognizing it even though it's quite clearly water vapor. Now given that a drug like LSD makes you more suggestable, and that it's already overloading your neurons in such a way as to cause you to see fractal patterns where none exist, then it seems logical that it would also overload the neurons relating to matching those patterns with known objects like faces, causing you to falsely associate your hallucination with the perception of a face or entity.
Anonymous
If you're interested in the subject Jack Cowan gave a talk at the Redwood Neuroscience center. The video lecture is online at archive.org.
Spontaneous pattern formation in large scale brain activity: what visual migraines and hallucinations tell us about the brain (2006)
Anonymous
When I hallucinate, I see equations and words on walls. Not fractals and patterns. I have no idea what this says about the contents of my subconcious mind, but it's interesting to think about.
Anonymous
I've had that with MDMA before, but only the one time strangely. I remember seeing a mess of equations and letters in the night sky, floating back and forth as hallucinations can do. Also saw crowns and diamonds ahah was a fun night though!
Anonymous
is silly. Correlation isn't causation. I have done many psychedelics, and I have never seen any of these patterns. Reminds me of an old person talking about "The Facebook" or whatever else you want to put in there. When it comes to awareness and consciousness, the western/Indo-European so-called "scientific" community is so far behind it thinks it's first. Sad.
Anonymous
is silly. The scientific community saves lives, can predict the future and can make awesome things like computers.
Gonfera Burton
When I drink lots of alcohol I get drunk. Correlation does equal causation in this instance. When I take psychedelics I see patters (hallucinations - because they are not actually there). I have seen Paisley print on my plain blue denim jeans. Just because you don't hallucinate doesn't mean others don't. I don't hallucinate without drugs (or fever). Therefore, I think it is fair to assume the the drugs are responsible for the hallucinations.
Anonymous
I have always been able to see my own mandala of geometric visual hallucinations from a very young age. Its just normal to me. I can see or tune into it whenever I want. It helps me meditate. I have also drawn a lot of art of geometric shapes and a couple have turned out to be optical illusions. My drawings arent planned out I just draw. I have been diagnosed with bipolar affective disorder since 2010 but even though I take medication I still have my geometric hallucinations. Its like checkerboards spiraling in all directions sometimes there are colours mainly green and red with bright yellow lines and sometimes i can just see the spiralling shapes of the checkerboards in black and white. I have taken hallucinagens in the past and they have made the hallucinations more extreme but I always have them. Like I say I can tune in whenever I wish. Id love to know more on this subject. I wouldnt mind being a test subject either. I personally feel more spiritual than scientific but Im open to answers as to why I have this phenomenon allll the time.
Anonymous
I've seen some pattern like these, not exact like those, but close. And it was an amazing feeling.
Anonymous
I have a relatively mild bipolar disorder but I function well i my job as physician and in my family. Five years ago, during a hypomanic phase, I began to see rounded, slightly irregular, honeycomb patterns with dark contours and paler areas and a black disc in the centre, while I had my eyes closed and focused on the dark behind my eyelids. When my mood normalized after a couple of months, the pattern disappeared. But the last year I can se the patterns on demand, though my mood is normal. I have begun to systematically study the phenomenon and have found that the honeycomb pattern with dark contours transforms itself constantly, so that some "cells" grow slightly bigger and other smaller in a calm way, like a living tissue. The pattern is strictly flat. After a while (a minute or so), I can see another type of pattern with swiftly moving short and straight and a little shaggy lines against a total black background. Those lines form rapidly changing complex forms of a more three-dimensional appearance, like pyramids, "bubble-gitters" and so on. If I continue the session, which is like a meditation for me, I have short flashes of photorealistic hallucinations in a limited area of the "visual" field. It can by human eyes, mouths or more complex and beautiful pictures with clear but somewhat dark colors, like old paintings. I have noticed that my ability to see the visions have improved during this year of regular practice. Now I try to paint the motifs and I feel the training is good for me and makes me feel more stable and focused i everyday life. It was nice to read your comment and interesting to share the experience. I don't use any drugs and for the moment no medication.
sven.lennart.a@gmail.com
Anonymous
i am curious what the brain means to you , given what we know about it in your opinion?
Anonymous
Hi, I just ran "The Toughest Foot Race in the World," which is 135 miles across Death Valley. I have run several ultras before, but this was the hottest and hardest. About 28 hours into my 39 hour run, it was dark in the desert and running on pavement. All the shrubs, rocks, geological features started to turn to bears, bison, people, motor homes, boats, etc. Those have happened before, but after another hour or two of running the pavement turned into millions of numbers, formulas, Indian symbols, chemistry elements, graffiti, etc. I knew these were hallucinations, but it was maddening. This pattern/hallucination ran from horizon to horizon. I hoped when the sun rose, it would reset my brain, but these "faux patterns" continued until sleep at the end of the race (2:00pm). Other than the obvious sleep deprivation and physical exhaustion, what caused this in condition in the brain? Any random set of features turned into words (in one case the moles on my pacer's face.)
I hope I never have this condition again...it reminded me of the "A Beautiful Mind" movie. It became increasingly confusing/irritation. Please send any answers/thoughts to Charlies@woodlandobrien.com
Thank you.
Scary, I had to do complete the verification that reminded me of the visual hallucinations!
Anonymous
The reductionist conclusion that such visions are "simply" reflective of the brain's wiring, along with the comments condemning the "absurdity" of the poster who indicated a metaphysical connection, has as its basis a false dichotomy - that is that these patterns cannot simultaneously reflect both the brain's wiring or structure and "part of what makes up our reality." Why can it not be both? In fact, I posit that that is indeed the case. My background is in math, and I experimented "back in the day" with LSD. What I have concluded is that the very real mathematical patterns we find in nature are those same patterns that are seen in induced hallucinations as described. The patterns that I saw when on LSD I now easily perceive throughout nature sans any "substantial help!" In other words, the patterns are easily observed without any induction. I would argue that these harmonious and integrated patterns that are found both in nature AND the brain are what allow perception, intelligible decoding of physical information around us, etc. In other words, the fact that there is some ordering principle that pervades the cosmos, ourselves included - our brains included, points to a cohesive framework of perception and intelligibility. I would further argue the metaphysical position that this ordering principle points to a transcendent reality and intelligence that pervades all of reality including the human person. I would call that intelligence "God," and am grateful that somehow we are connected to it all!
Ted
Great answer. I couldn't agree more..much evidence exists for spirals and elegant geometry in nature. Fibonacci numbrs/Golden ratio, tiling as studied by Penrose and Mandelbrot sets demonstrate the ubiquitous nature of the spiral. Clearly the universe is imbued with elegance in form and function which shows up across scale...spirals in atom smashing and spirals in galaxies...pine cones, sunflower heads..everywhere and both inside and outside our brains.
Xyinyl
First let me say I have NEVER taken drugs. EVER, meaning hallucinogenic type. I have migraines so I do take an over the counter migraine tablet daily. But in the last few years I have seen images of advance math on walls, furniture, almost everywhere, almost like graffiti. I am a high school grad with some college. Terrible at math and don't understand what I'm seeing. I've looked on the internet regarding the images and have come very close to finding what I'm seeing but not finding why I'm seeing it. Does it have something to with migraines? Triangles and letters in fractions, wiggly equal signs, cursive capital letters with plus signs and lesser and greater symbols. I'm hoping I'm not going nutty. Does anyone have a clue as to what this might be? I've searched and searched. A little hesitant to tell anyone.
Dave
I read this article because I have been taking all different psychedelics for the last 26 years & the reason I read it was because everytime I trip, there's a point of time , be it 5 minutes to 5 hours where everything whithins my eyes range I can see broken down mathematically , now I don't mean different geometric patterns , but just say there is a chair sitting in front of me , suddenly i start visualizing each leg almost as if it was made of glass or a c.a.d. Blue print drawing of it, I see the legs all 4 at once & I can see that they are each 1 1/8" wide at the base but the measurement at the top where it holds the seat its 3/4" wider , i see the measurements themselves a lot of the time , but sometimes they're just the shapes & I somehow know the size differential. Next I start seeing the seat, the brackets that hold it together , the screw holes & their diameters , the back of the chair , & the weird thing to me was always like , how do I even know some of these shapes exist ,lol. So anyway , I'm looking for any article to explain the way the brain ,( if it's not just me) breaks down all of these things so perfect & intricately. Thanks
Raz
This, I once entered this empty "developer mode" I described it on an lsd trip, whatever I thought of I could see super detailed schematics for it. I wonder if like Leonardo Da Vinci could see things like this when he came up with his machines..It was super interesting to say the least.
ELENA
I have been seeing fractals for some time now, no, i don't trip on anything at all, I started doing breath work and since then I have noticed that I was seeing fractals when I rubbing my eyes, now I see them by just closing my eyes, no need to rub them to see them any more. I am just very curious as to why this happens so I am trying to get my hands on whatever information I can find to learn more about it.
Valarie
I've been seeing this since I was a little girl. I still do and its been getting stronger since I had my babies. Let me know if you find more info
Lisa Baker
Hi, I've been seeing them since about 1st grade myself. I became more aware of them in the last few years while going through visual therapy exercises. You can find me on Facebook as PatternNerd. If you ever want to discuss I'd love to hear from you.
amylynne
This article is in 2009 but I am just reading now in 2019. I have always seen floating pattern mandala-like but more random not symmetrical. Most often in the dark or when I close my eyes. I just always thought that was what darkness is or made with. I have never met anyone else who describes this until I read the comments. It is nice to know it is not uncommon and I feel more comfortable now that others see them also.
russ worthy
very helpful article and explains quite a bit.
Al
I found this because once years ago I smoked Hashish and only in hindsight it seems like I passed out in my chair, and my mate woke me up saying my lips were blue. But what I experienced at the time was like a kaleidoscope of brown and purple, and then my mate saying my name and then I came round and was back in the room. It was trippy as balls! And I've smoked weed a lot since, it's never happened again, but was always curious what that was. I saw a Mandala in some talk about consciousness, and then I found out about form constants. Whatever it was, and whether the justification you want to assign to it is mathematical or spiritual, it doesn't matter, it happened, maths is just an attempt by humans to describe something accurately, but what does that description really bring to the table in terms of understanding not many answers I conclude, (which is fine by the way)
Hugo Koch
This string theory PhD doesn't understand the brain whatsoever. Hallucinogens are enzyme inhibitors and thus they turn off neural functions. The true reason you "hallucinate" is because your mind is opened to greater information of our reality. Hallucinations are not "not real". All things that appear in consciousness are real including thoughts. Don't confuse reality with physicality. The self has no physical origin, i.e. the brain does not produce consciousness. If you think that matter becomes self-aware by moving it around in some mysterious way, i must, from nothing comes nothing. Shut your stupid mouth.
Agnes
Yeah I can see these patterns whenever I tune in. Doing so can cause me to almost instantly fall asleep, in fact. (And I am otherwise an insomniac). I always thought of it as my brain processing visual data, and that the more pronounced it gets, the more exhausted / "full" my mind is thus the more in need of its time to just rest / process.
Anonymous
I Have experimented with LSD a multitude of times over the years, a common occurrence for me is I will see visuals that are a combination of numbers, runes/letters, and symbols which I see just about everywhere etched into walls, skin, objects etc. two symbols I see pretty commonly I have sketched while dosing and later identified them as the sonnenrad/Sunwheel and the other Symbol being vegvisir. Anyone have similar trip experiences?
Rachel
Interesting and informative article, but the omission of Bresslof’s wife’s name adds to an ugly history of the erasure of women’s scientific contributions.
Mariana
Completely agree, I wanted to search for her but is sad that the only woman in this article has no name :/
Really good article, though
Stoodley
All I know is that when I tripped this is also what I saw, surrounding and emanating from a house fly, notably…and was pretty much everywhere I looked. He’s gone now but left me with a shit load of hard drives. I still don’t know how he managed to spend most of his life on something he wasn’t able to explain to me. He just said,” it’s the same stuff you see isn’t it. Maybe that’s all he needed to say.