Can maths reveal new phenomena in biology? Jacques Dumais, from Adolfo Ibáñez University in Chile, and Etienne Couturier, from Université Paris-Diderot in France, think that it can.

The power of maths has already been demonstrated in mathematical biology, where mathematical models are inferred from quantitative biological data. For example, the empirical models from epidemiology have allowed the medical community to combat and sometimes even eradicate infectious diseases. What Dumais and Couturier are seeking, however, is slightly different. Dumais says they aim to distill underlying biological principles from observations, allowing them to predict new things in biology.

"Theoretical biology is closer to theoretical physics – where the mathematics is formal enough that you can begin predicting things that have never been seen or measured," says Dumais. They hope to uncover mathematical descriptions of biological processes and that these biological laws will allow them to predict and observe previously unknown phenomena, in a similar way to the great insights that theoretical physics has made to our understanding of the physical world.

Divide and conquer

As an example of the possibilities this approach could bring, Dumais told the British (Applied) Mathematical Colloquium, in Cambridge last month, how the geometry of plant cells drives cell division. This is not a new area of research: in the nineteenth century two biologists put forward rules for cell division. In 1875 Julius Von Sachs came up with two rules: that when a cell divides it creates two daughter cells of equal sizes; and that the new cell walls will meet the old cell walls at angles of 90 degrees. Around a decade later Léo Errera proposed another rule that the new wall created by the dividing cells would be as small as possible (in fact, it would mimic the action of a soap-film, which minimises surface area).

Dumais and his colleagues were able to formalise these growth rules and show that just two of these rules – minimising the length of the new cell wall and creating cells of equal area – were necessary. The third rule – that the new wall will meet the old cell walls at 90 degrees – comes out as a mathematical consequence of the other two.

The redundancy of this third rule had already been noted much earlier, says Dumais. But their work has shown that these rules, which are an accepted part of plant biology, are mathematically self-consistent: there are no conflicting predictions from the different rules. "Self-consistency gives strength to the argument that these are fundamental rules," he says, something that is essential for building up a formal mathematical framework.

On the left is a micrograph of the cellular pattern of Coleochaete (image courtesy of P. W. Barlow, first appearing in Cell Proliferation), on the right is the cellular pattern predicted by the mathematical model (image courtesy of S. Besson and J. Dumais).

Dumais and his colleagues tested their model for cell growth and division against the patterns observed in Coleochaete, a simple two-dimensional alga whose cells only grow and divide at its circular perimeter. Each outer cell has the form of a truncated wedge, allowing the researchers to precisely characterise the shape of these cells.

They described the shape of each cell by the angle, , between the two straight walls of the cell (as if these walls ran all the way to the centre of the plant), and the ratio of the cell's length over the radius of the whole plant at this point. Cells grow in length, until they divide in one of three ways: along the wedge (indicated in blue in the image below), across the wedge (red) or occasionally across one corner (green).

With their geometrical description of the possible cell shapes, and the two division rules formalised mathematically, their predictions for the growth of Coleochaete closely matched reality. (You can read more in their paper.)

Moving towards fixed points

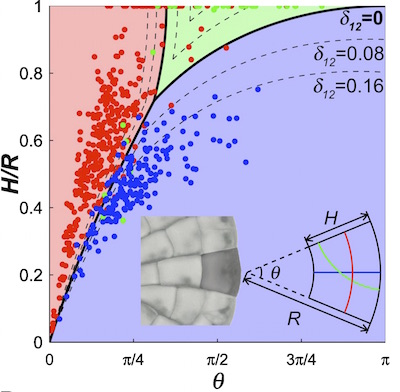
The dynamical system for the growth and division of Coleochaete cells. (Image courtesy of J. Dumais)

Dumais and his colleagues were able to predict the cell division and growth of the Coleochaete and other plants by viewing the future of each cell as part of a dynamical system – something that changes over time. They considered the whole range of geometrical shapes a plant cell can take, and then applied the mathematical cell-division rules to predict how the shape of that cell and its daughter cells will change over time.

For example, for the dynamical system for Coleochaete, all cells must fall within a two-dimensional space of possible cell shapes. This space is mapped by two axes: a vertical axis for the height/radius ratio and a horizontal axis for the angle of the wedge. The cell grows and divides, and the resulting changes in shape for it and its daughter cells trace out a path through the space of possible shapes. Most wide cells would divide along the wedge (blue in the image of the dynamical system on the right), most long cells across the wedge (red). They then lengthen (move up along the axis) until they divide again.

For all cells, the shape of their successive daughter cells tend towards the shape described by the boundary of these blue and red regions, and then along this boundary towards the origin where the two axes meet. Cells located near the origin in this space have a very small angle and a height that is small compared to the radius of the plant. Not surprisingly, this is the similar uniform shape that appears at the outer edge of the alga.

Mathematically the dynamical system for the Coleochaete cell shapes tends towards this shape because it is an attracting fixed point. A fixed point of a dynamical system is a state such that when an element in the system achieves that state, it then stays in that state forever. In the case of the plant cells, a fixed point is a shape such that once a cell achieves that shape, one of its daughter cells will also have that shape. This occurs when the application of the two division rules results in some sort of self-similarity between the mother cell and the daughter cell.

"You can write down the equations [describing these dynamical systems] explicitly and find the fixed points," says Dumais. The researchers did this for a wider variety of plants, where a central cell (called an apical cell) dominates the growing process, remaining at the main point of growth, continually dividing to produce daughter cells. As more cells are produced, the previous daughter cells move away from the apical cell and may themselves divide. These packets of cells, all descendants of a particular daughter cell, always retain the imprint of the shape of this original daughter cell.

When considering all the possible shapes such apical cells could take, Dumais and his colleagues mathematically predicted five possible fixed points where the division rules created identically shaped daughter cells. Each of these fixed points is distinguished by the number of sides they have

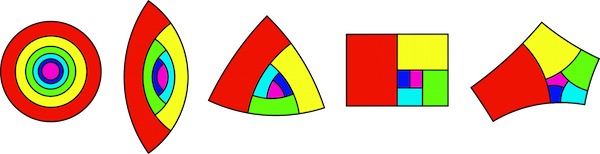
The five fixed points for cell division of apical cells. The pink shape is the apical cell that remains at the central main point of growth while continuing to divide. The other coloured shapes are the daughter cells, that move away from the apical cells as more daughter cells are produced. The red shape is the oldest of these daughter cells shown in this picture, the dark blue the youngest. If the four-sided example looks familiar, that's because it is the same shape as the A paper format! (Image courtesy of J. Dumais)

A biological Higgs boson?

This was a satisfying validation of the researchers' mathematical model, as they were already aware of the existence of several plants with cells that matched these fixed points. "We had already seen the 2- and 3-sided cells," says Dumais. "We hadn't seen the 4-sided cells [before our prediction], but we found two examples of that." That only left the elusive 5-sided fixed point yet to be seen in nature. Perhaps this will be the Higgs boson of biology, predicted mathematically before it has been observed in nature? Perhaps, but probably not, says Dumais. It's very unlikely we'll ever see such a shaped cell growing naturally as the researchers believe the 5-sided cell may not be a stable fixed point under realistic biological conditions. The other four fixed points are attractors, the daughter cells of cells close in shape to these fixed points become closer and closer in shape to these fixed points (you can read more about stable attractors here). In contrast, it seems that cells even slightly different in shape to the 5-sided fixed point may end up as having a very different shape.

The elegant simplicity of this mathematical model of cell division is an example of the approach that may be necessary to succeed in theoretical biology. "In biology, in contrast to fluid mechanics or physics, there is very noisy, unreliable data," says Couturier. "If you make a complex model often it won't work, it won't be stable enough. In general if you want to do something meaningful you have to take a lot of time to identify something you can treat with a simple model." For biology, and the messy data it provides, you need simple tools.

This may make the field even more attractive to mathematicians, who often feel the simpler and more elegant the model, the more insightful it is. And as well as beautiful mathematics, if theoretical biologists are able to distill biological processes into such models, Dumais believes it will bring great insights to biology itself. "Biology will gain a lot. What's missing now in biology is a framework to explain or organise all the information that we have." And just as theoretical physics successfully predicted the existence of fundamental particles, such as the Higgs Boson, before their experimental confirmations, we look forward to the exciting horizons theoretical biology will reveal in the natural world around us.

About the author

Rachel Thomas is Editor of Plus.