
Counting on connections
Congratulations to our neighbour, Julian Sahasrabudhe, assistant professor in the Department of Pure Mathematics and Mathematical Statistics at the University of Cambridge, who has been awarded a Whitehead Prize by the London Mathematical Society! His Whitehead prize recognises "his outstanding contributions to Ramsey theory, his solutions to famous problems in complex analysis and random matrix theory, and his remarkable progress on sphere packings."
These areas of maths might at first seem quite disconnected. But Sahasrabudhe has been able to use his background in combinatorics – the area of mathematics that studies how we can count or arrange things – to make significant progress in each of these areas.
"Combinatorics has reached this really interesting point where there's enough theory that it's able to jump and connect to other areas," says Sahasrabudhe. He is particularly keen to make these links: "to take something I find really interesting but don't understand, and understand it with the tools that I do."
Packing spheres
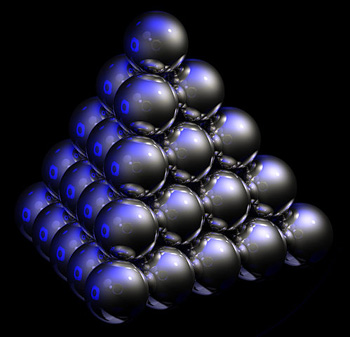
This is the face-centred cubic packing – the one of those suggested by Kepler. It is one of a number of packings that are equally good in three dimensions at filling the most amount of space. Image: Greg A L, CC BY-SA 3.0.
A good example of this approach is sphere packing. This classical problem can be thought of in terms of packing oranges (or cannon balls, or any other sphere-shaped thing) in a very large box. What is the maximum number of oranges you can fit in the box, what is the best way to pack them, and how much of the volume of the box will they fill? This became known as Kepler's conjecture after it was formulated mathematically by Johannes Kepler in the 17th century. Kepler suggested a packing of oranges that would fill about 75% of the box and over time mathematicians discovered several other packings that were just as good. But it took centuries to prove this is the best you can do.
Kepler's conjecture was finally proved by Thomas Hales in 1998, but it took a 250 page proof that relied on gigabytes of computer code and data to churn through the difficult cases. "This is an incredibly difficult theorem to prove in three dimensions," says Sahasrabudhe. "And when you go to higher dimensions it's a complete mystery."
Higher dimensions
It might seem very esoteric to think of packing higher dimensional spheres into higher dimensional boxes but for mathematicians it is an obvious next step. While we struggle to visualise things spatially in more than the three dimensions, Sahasrabudhe says we're actually very used to this idea. "Each dimension is really just a measurement. I can describe any point in a square in terms of two coordinates: length and height. And going from two dimensions to three, I can describe any point in a cube with three numbers: length, height and depth."
Just as you can extend the concept of a square in two dimensions to a cube in three dimensions, you can extend the concept to even higher dimensions, such as to a tesseract or four-dimensional cube. "I can easily go to higher dimensions," says Sahasrabudhe. "To describe any point in four dimensions I just give you the four numbers."
Similarly we can extend our concept of spheres, and sphere packings, to higher dimensions. We now know the best way to pack spheres in dimensions 8 and 24, thanks to the work of Fields Medallist Maryna Viasovska. These sphere packings had been thought for some time to be the best in those dimensions but it took an amazing method Viasovska developed in 2016 to prove that they were. The work was a huge step forward but it didn't give any clues on how to find the best sphere packing in higher dimensions. "It only works for these magical dimensions of 8 and 24," says Sahasrabudhe. (You can read an easy introduction to Viasovska's work here.)
Mathematicians wanted a general method that would give a good candidate for sphere packings in any very high dimension. In 1947 Claude Rogers showed that, in very high dimensions, using a particular type of lattice arrangement for the spheres was denser than any other known packings at that time. In 2023 Sahasrabudhe and his colleagues, Marcelo Campos (University of Cambridge), Matthew Jensse (King's College London) and Marcus Michelen (University of Illinois, Chicago), improved on Roger's result, giving a general method that produced sphere packings that were even denser.
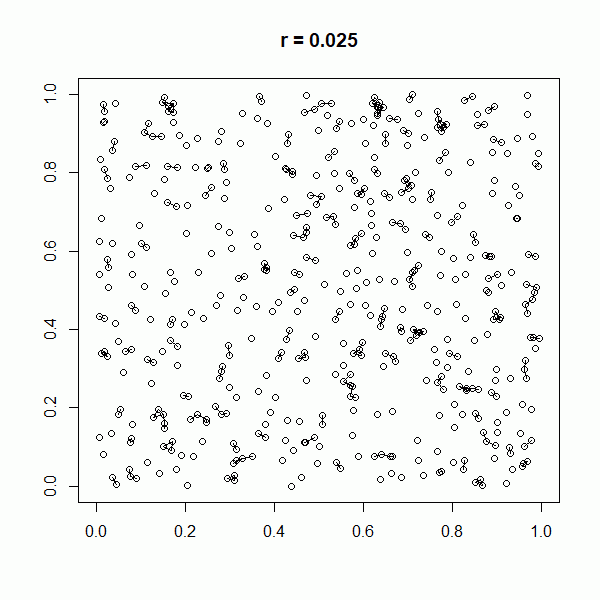
"What's interesting about our packings is they are very random, they don't have any periodic structure." This is very different to the regular lattice used by Rogers. And also very different to what happens in lower dimensions where the best packings are also very regular: the honeycomb arrangement of circles in two dimensions, and the regular arrangements of spheres that are densest in three dimensions, such as the traditional way oranges are stacked in a market stall.
Sahasrabudhe and his colleagues, none of whom came from a geometric background, instead used a very new way to construct their sphere packings. They started with a random arrangement of points in space, and then joined points that were near to each other with a line. This created a graph, a common object of study in combinatorics. "We really turned it into a combinatorial problem and then solved this." They applied techniques from graph theory to transform this initial graph into one that represented a dense sphere packing. "We took away all the geometry rather quickly and dealt with something which is much more familiar to us."
Friends and strangers
Sahasrabudhe's Whitehead prize also recognises his outstanding contribution to an area of combinatorics called Ramsey theory. "One of the slogans of Ramsey theory is that complete disorder is impossible," he says. If you have an arbitrary system of some type, Ramsey theory is interested in what order you can find in that system. For example, suppose you have any randomly selected group of people, some of them might know each other, some of them might not. Can you say if the group includes three people who were all friends, or all strangers? (You can read a short introduction to Ramsey theory here.)
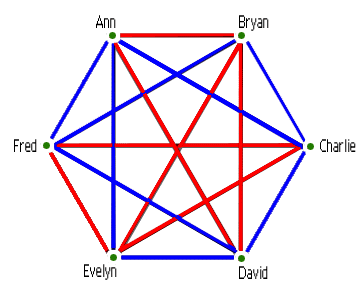
A group of friends, linked by a blue edge if they are friends and with a red edge if they are strangers. How big does your group of friends neeed to be to guarantee three people who are all friends (a blue triangle) or three people who are all strangers (a red triangle)?
A key idea in Ramsey theory is that you can always find such ordered substructures, as long as your system is large enough. But how large does a system need to be to guarantee that you find order? The answer to this question for the friends and strangers problem is called a Ramsey number. The Ramsey number, R(3,3), is the size your group has to be to guarantee you have three people who are all friends, or all strangers, and we know that R(3,3) is 6. We also know the Ramsey number R(4,4) is 18, that you need a group of 18 people to guarantee that you have a subgroup of four of them who are all friends or all strangers. But we quickly get stuck after this. For example we don't know what R(5,5) is. We know it's somewhere between 43 and 46 but that's as close as we can get for now.
One way of understanding these Ramsey numbers is to try to understand how quickly they grow. In 2023 Sahasrabudhe was able to prove important new results about this growth, again working with his colleague Campos, along with Simon Griffiths (now at PUC-Rio University) and Robert Morris (now at IMPA). But it wasn't straightforward: "We spent a long time failing to get our approach to work and we had to rely on our intuition that we were going in the right direction… This is one of the most exciting things about mathematical research. When do you keep going? When do you give up? I think part of our success is that my co-authors and I have a pretty high tolerance for failure."

Collaboration has become an increasingly important part of Sahasrabudhe's mathematical approach. "I've really found really good groups to work with. You kind of keep each other company through the [work], everyone that I've been working with recently is a good friend. We also just enjoy hanging out together and I think that really helps as well."
Whitehead prizes are awarded by the London Mathematical Society to recognise outstanding work by mathematicians at an early stage in their career. This is fitting, as Sahasrabudhe now recognises his role in helping to support the next generation of mathematicians. "The culture of supporting and educating students and young researchers is one of the things that's really good about Cambridge – it makes it a pretty special place." We look forward to seeing what Sahasrabudhe, and his colleagues both young and established, go on to do next.
About this article
Julian Sahasrabudhe is assistant professor in the Department of Pure Mathematics and Mathematical Statistics at the University of Cambridge.
Rachel Thomas is Editor of Plus.