
Packing spheres
When it comes to transportation fruit are awkward. Not only are they easily squashed, they also have shapes that don't lend themselves to being packed in boxes. Even the simplest possible fruit shape, the sphere as seen in oranges and apples, causes a problem, because no matter how you pack spheres, there'll always be gaps between them. This raises a geometrical question: how should you pack spheres into a box to make sure the volume of the gaps is as small as possible?
This month we met an expert in the field: the mathematician Maryna Viazovska who in 2016 made a breakthrough in the theory of sphere packings. She explained her results at the Royal Society's celebration of the legendary mathematician Srinivasa Ramanujan, who was elected a fellow of the Society 100 years ago. During a coffee break she gave us a condensed description of sphere packing problems and her work. (You can also listen to the interview in a podcast.)
The problem
"Suppose you have a very big box and a supply of spheres," Viazovska explains. "To make the problem easier suppose the spheres are of equal size and also hard, so we cannot squeeze them. We put as many spheres as we can into the box." The question is, what's the largest number of spheres you can fit in?

The hexagonal circle packing.
If the box is small, then the answer depends on the shape of the box. But if the box is very large, the effect of the shape is negligible, and the answer depends only on the volume of the box. "It's intuitively clear, though mathematically one has to work a little bit to see this, that there is a maximal possible [proportion of the volume you can fill with spheres]." The sphere packing problem is to find this highest proportion, also called the sphere packing constant.
For an easier example, let's drop down a dimension: instead of packing spheres into 3D space let's pack discs into 2D space. "In dimension two the best packing [comes from the] honeycomb," explains Viazovska. In a traditional honeycomb every cell is a hexagon and the hexagons fit neatly together leaving no space between them. If you arrange discs in the same pattern you do get gaps, but the packing turns out to have the highest density possible. "This way we will cover slightly over 90% of the area with these equally-sized discs." The precise value of the sphere packing constant in two dimension is $$\frac{\pi \sqrt{3}}{6} \approx 0.9069.$$ "In dimension three [the problem] was known as Kepler's conjecture and remained open for [nearly 400] years," says Viazovska. "[Here] we don't have only one best packing, we have many equally good packings. One of them you can see on the market, where oranges are stacked in pyramids (see the figure below, which illustrates this with balls rather than oranges). The density [of this packing] is about 74%." The precise value of the sphere packing constant in three dimensions is $$\pi/(3\sqrt{2}) \approx 0.7405.$$
The proof that you really can't do any better than this only arrived in 1998 when the mathematician Thomas Hales produced 250 pages of traditional mathematical proof supplemented by over 3 gigabytes of computer code and data for making necessary calculations. This was a controversial approach. Since no human could possibly check the computer calculations in their life time, mathematicians weren't sure if Hales' work really counted as a proof. A panel of experts eventually decided they were 99% sure that it did, and since then the proof has been verified using formal computer logic.
Higher dimensions
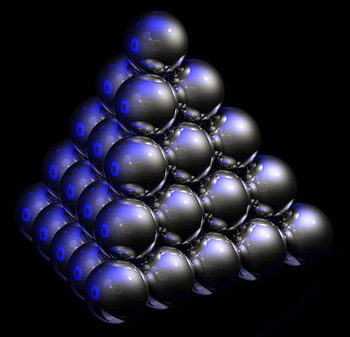
This is the face-centred cubic packing, one of the packings with maximal density in dimension three. Image: Greg A L, CC BY-SA 3.0.
Involving no computers and filling just a few pages, Viazovska's proofs are as solid as proofs can get. They involve packing higher-dimensional spheres into higher-dimensional spaces, namely spaces of dimensions 8 and 24. The endeavour might seem both useless and impossible to get your head around, but it's neither. Higher-dimensional sphere packings are important in communications technology, where they ensure that the messages we send via the internet, a satellite, or a telephone can be understood even if they have been scrambled in transit (find out more here).
To get a grip on higher dimensions, cast your mind back to school when you moved from doing geometry in two dimensions to doing it in three. If you were one of the many people who struggle visualising things in 3D, you'll have appreciated the help of algebra. Points in three dimensions are given by three coordinates, and shapes such as lines, planes or spheres by equations involving the coordinates. If you can't visualise how shapes relate to each other, you use the equations to help you.
In higher dimensions the same principle applies. Points in $n$-dimensional space are given by $n$ coordinates. You can come up with notions for distance and volume in analogy to two and three dimensions, and you can define shapes, such as spheres, using equations. Although you can't visualise these shapes, the algebra allows you to deal with them, so you can also define what you mean by a sphere packing and its density.
Going back to the familiar dimensions two and three for a moment, you can see how a 3D packing can be made from a 2D one by stacking: start with spheres arranged in the honeycomb pattern that gives the best density for circles in 2D and stack another layer of spheres above it, so that the spheres of the second layer sit in the dips between spheres in the first layer. Then add a third layer, and a fourth layer, etc. This does generate a 3D packing with optimal density, so it's tempting to think that stacking might also work in higher dimensions.
Alas, it doesn't. Knowing the densest packing in one dimension doesn't give you a clue of what it should be in the next. The graph below shows the density of the densest packings we know for dimensions 4 to 26, but these might not be the densest overall. The graph suggests, and this turns out to be true, that the sphere packing density decreases exponentially as the dimension increases.
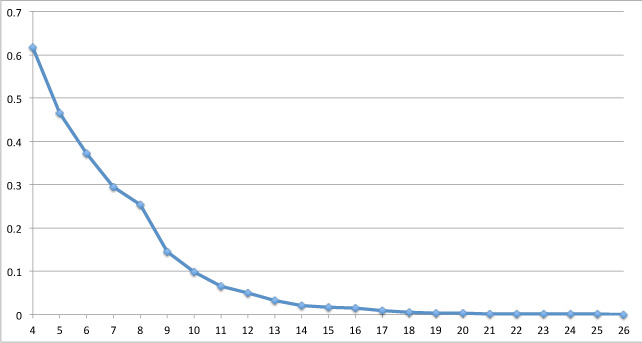
The density of the best-known sphere packings in dimensions 4 to 26.
Finding bounds
When you're trying to find a number that attains some sort of a maximum, like being the highest packing density, but haven't got much luck, one approach is to lower your bar and look only for an upper bound: in our case a number you can prove the packing constant can't exceed.
Various upper bounds for packing densities have been known for some time, but in 2003 Henry Cohn and Noam Elkies came up with a particularly interesting recipe for finding them in any dimension. The recipe is hard to put into practice, so Cohn an Elkies were only able to approximate the associated upper bounds for dimensions up to 32. The result is shown in the graphs below, together with the best-known values for the packing density, for dimensions 4 to 12 and 20 to 28.
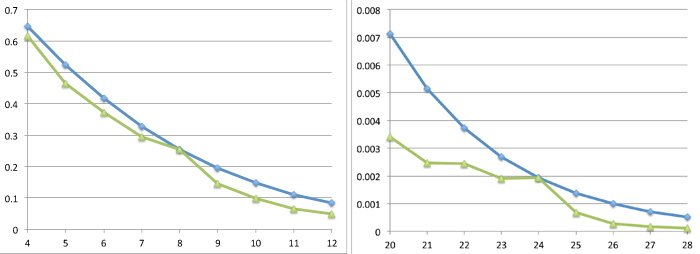
The Cohn-Elkies upper bound (blue) and the density of the best-known packing (green) for dimensions 4 to 12 and 20 to 28.
What's striking here is that in dimensions 8 and 24 the two graphs appear to coincide. If they really do coincide, then the densest packings we know in these dimensions are also the densest overall, and their density will be the sphere packing constant. But Cohn and Elkies weren't able to prove this: there remained the annoying possibility that denser packings exist, whose densities fall right into invisibly tiny gaps between the two graphs. "That's not a plausible scenario for anyone with faith in the beauty of mathematics, but faith does not amount to a proof," Cohn wrote in a beautiful (though more advanced) article in the Notices of the American Mathematical Society.
Closing the gap
Viazovska's work, which closed the gap for dimension 8 and was later extended with the help of Cohn, Abhinav Kumar, Stephen D. Miller, and Danylo Radchenko to dimension 24, builds on the centre piece of Cohn and Elkies' work. If you forget about the actual spheres in a sphere packing and only consider their centres, you're left with a configuration of points. Rather than giving the coordinates of all the points, you can also characterise the configuration by the statistics of the distances between points: what is the smallest distance that occurs, how often does it occur, etc.
The E8 lattice sphere packing
The spheres in this eight-dimensional packing are centred on points whose coordinates are either all integers or all lie half way between two integers, and whose coordinates sum to an even number. The radius of the spheres is $1/\sqrt{2}$.
The E8 lattice is related to the exceptional Lie group E8. As the name suggests the group is an exceptional object in mathematics, so it's perhaps not surprising that it is connected to an exceptional sphere packing.
It's a fruitful approach that is often used in physics. "Astronomers also do this," explains Viazovska. "They look at the stars and compute the distances between different stars and then forget about the geometry of space and remember only the statistics of pairwise distances. It turns out that these statistics have to satisfy certain restrictions. If you want to have so many stars at this distance, and so many stars at that distance, and so many stars at another distance, it might not be possible to realise this in space."
In a similar spirit, Cohn and Elkies had shown that the distance statistics for a sphere packing should also satisfy certain restrictions, which in turn give an upper bound for a packing's density. To be sure the restrictions are really satisfied, though, you have to find a mathematical function with particular properties, and that's not easy to do. Cohn and Elkies were only able to approximate these functions, which is why they could only approximate the upper bounds you can theoretically get from their recipe.
To find the sphere packing constant in dimension 8 (and later 24) Viazovska had to take a step further. She had to find a "magic function" which not only gives you an upper bound, but also shows that this upper bound is sharp, in other words that it equals to the density of the best packing we know in dimension 8. Cohn and Elkies thought that such a function must exist, but had no idea how to find it — "The magic functions seemed to come out of nowhere," Cohn writes in the article quoted above.
This is the trick Viazovska managed to pull off: using a "bold construction" nobody had thought of before, she came up with a function that behaved just as required. The construction uses mathematical objects called modular forms, which were studied extensively by Ramanujan. This is why we met Viazovska at a conference celebrating the Indian genius.
With her result Viazovska proved that the highest possible density of a sphere packing in dimension 8 is $$\frac{\pi^4}{384}\approx 0.25367,$$ which means that around 25% of 8D space can be filled with non-overlapping spheres of the same size.
The packing which gives this density (and is marked as the best-known packing in the graph above) is called the E8 lattice sphere packing. We can't visualise it because it lives in eight dimensions, but we can describe it quite easily via the coordinates of the centre points of all the spheres — see the box. The packing that gives the highest density in 24 dimension is called the Leech lattice sphere packing. It's similar to, but more complex than, the E8 lattice packing, and its density is
$$\frac{\pi^{12}}{12!} \approx 0.001929.$$
Where next?

Maryna Viazovska. Photo: Petra Lein, CC BY-SA 2.0 DE.
The obvious next question is whether similar techniques can prove sphere packing constants in other dimensions. The answer, sadly is, no. "For other dimensions the method of Cohn and Elkies gives some bound, but the bound is not optimal," says Viazovska. "Everybody asks what is special about dimensions 8 and 24 — I don't know, it's a mystery. In these dimensions we have these two extremely great configurations, which we don't have in other dimensions. They are so good that methods which fail in all other dimensions in these dimensions give a sharp estimate. If you ask me why, I don't know."
Not all is lost, however. Cohn and Elkies approach hinges on a deep result (known as the Poisson summation formula), but doesn't make use of all the information the result could theoretically give you. "There are many inequalities the statistics [of pairwise distances] have to satisfy," explains Viazovska. "Theoretically we know all these inequalities, but describing them is quite difficult." For dimensions 8 and 24 it's possible to get away with only two of these inequalities, but for other dimensions we might need more. "One way to go would be to use those additional inequalities. I'm working on this, but it's not all that easy."
Another approach would be to make better use of the geometry of sphere packings, which was ignored in Viazovska's proofs in favour of statistics. "Maybe in some dimensions [forgetting the geometry] is not such a fruitful idea," she says. "Maybe we should come back to geometry, or use a combination of methods."
"In other dimensions we know that there are [packings] that are good and people keep records of them. In small dimensions, up to ten, people are quite confident that the [packings] we think are the best. But of course as the dimension increased, our confidence decreases — it decreases exponentially."
About this article
Marianne Freiberger is Editor of Plus. She interviewed Maryna Viazovska at the Royal Society's celebration of the centenary of the election as a Fellow of Srinivasa Ramanujan. She would like to thank Alison Kiddle for her take on higher dimensions.
You can also listen to the interview in a podcast.
Comments
Chris G
"no matter how you pack spheres, there'll always be gaps between them" Para 1
What this suggests to me is that no matter how many rigid 3D same size (or even different size maybe) spheres you stack together as densely as possible, there will always be space enough for an ant to crawl about absolutely anywhere in the stack. Is that so? Has it already been conjectured and/or proved? (I've already started experimenting)
This doesn't apply to circles in that 3 tangent circles can completely enclose and block off the space between them so that there's no passage into it, at least not in the same plane.