Eat, drink and be merry: making sure it's safe

Back to the Next microscope package
Back to the Do you know what's good for you package

Most mathematicians have a perennial problem when they are asked to justify their existence at a party. How can maths be of any use, is a commonly asked question. However, in the context of a party, where we all know that good food is vital, maths is an essential ingredient. In fact, maths is vitally important to the food industry and many of the processes of dealing with food. From farm to fork, and from fork to (sorry to be crude) the sewers, maths is there. It explains and models the processes which govern the safe production, storage, testing, transport, cooking, eating and digestion of food (and indeed of pharmaceutical drugs). In particular it helps decide whether and how it is safe to cook, eat and digest a food stuff.

There's lots of maths in chocolate and it tasted good, too!

In this series of two articles I will have a look at two ways in which mathematics comes into food, and especially into food safety and health. In this article we will look at how maths can tell us the safest way to cook food (in a microwave oven). The other article takes a dive into the rather smelly business of digesting food, and how a crazy application of chaos theory shows the best way to digest a medicinal drug.

Lest the gentle reader think that this is all a bit of a waste of everyone's time and is not a serious application of science, ponder on the humble biscuit. A lovely application of mathematics helps to predict when biscuits crack, and can thus reduce the chance of them cracking when they are made."So what," said the Today Programme interviewer when confronted with this amazing fact. Well, it so turns out that the biscuit industry and ancillary food industries employ 1.5 million people, represent 15% of the total UK manufacturing output and annually contribute over £1Bn to the UK economy, and, be honest with yourself, would you buy a packet of cracked biscuits?

Cooking food in a microwave oven

A domestic mode-stirred microwave oven with four temperature probes used to test the predictions of the model.

As any student (or indeed hard up professor) knows, a popular way of cooking (or at least of heating) food is to use a microwave cooker. In such a cooker microwaves are generated by a magnetron (also used in radar sets) and enter the oven cavity via a waveguide or an antenna. An electric field is then set up inside the oven which irradiates any food placed there. The microwaves penetrate the food and change the orientation of the molecules in the moist part of the food leading to heating (via friction as the molecules vibrate against the other molecules in the food) of the foodstuff and consequent changes of water in the food into steam.

A problem with this process is that the field can have standing wave patterns, which can result in localised "cold spots" where the field is relatively weak. If the food is placed in a cold spot then its temperature may be lower there and it will be poorly cooked (see figure). This has very significant implications to public health. If the food is not hot enough, then bacteria in it will not be killed and this can then lead to severe food poisoning. To try to avoid this problem the food can either be rotated through the field on a turntable, or the field itself can be "stirred" by using a rotating metal fan to break up the field patterns.

A thermal camera image of food in a domestic turntable oven, showing a distinct cold spot in the centre caused by a local minimum in the radiant electro magnetic field. This can leave to very uneven cooking with potentially dangerous consequences.

Using mathematics we can model the process by which the food is heated in the oven and compare the effectiveness of the turntable and mode-stirred designs of the micro-wave oven. To do this, we need to do three calculations. Firstly we need to find the electromagnetic field in the food due to the microwaves. Secondly we have to work out how this field heats the food up. And thirdly we have to work out how much of the water in the food turns into steam during the cooking process. Noting that many foodstuffs are initially 80% water, the latter is a major part of the calculation.

The hard way

One way to approach this process of calculation is to simulate the full three-dimensional electric field by solving Maxwell's equations for electromagnetic radiation. Using this we can then find the temperature by solving another set of equations, the porous medium equations for a two-phase material, which is (typically) a mix of starch and water.

The problems with this approach are firstly that the computations take a very long time (often several hours!) and are often unreliable and difficult to verify. This makes it hard to see what happens when you vary the parameters in the problem, such as whether the food is on a turn table or a mode-stirrer oven is used. Secondly, this method gives little direct insight into the process and the way in which it depends upon parameters. Thirdly, micro-wave cooking is very sensitive to small changes in the geometry of the cavity, the shape and type of the food and even the humidity of the air. This means that any one calculation may not necessarily give an accurate representation of the electric field of any particular micro-wave oven on any particular day.

The easier way

What is more useful is a representative calculation of the average behaviour of a broad class of (domestic) micro-wave ovens in which the effects of varying the various parameters is more transparent. This is very often how a mathematical modelling approach can be very effective: a little mathematics can solve hours and hours of computer time, as well as often giving a more accurate answer.

Now, contrary to popular myth, microwaves do not cook food from the inside. Instead they penetrate from the outside and are absorbed as they pass into the foodstuff, losing energy as they do so. The hottest part of a food cooked in a microwave oven is usually just below the surface. If the food is too large, then the interior can receive almost no micro-wave energy, and as a result little direct heating. This is why the manufacturers of micro-wave cookable foods generally insist that, after a period of heating in the oven, the food is stirred to ensure that it is all at a similar temperature.

To model what is happening, let's imagine we are sitting at a point $(x,y,z)$ on or in our bit of food at time $t$ of the microwaving process. (We will think of the $x$ -coordinate as the depth into the food.) Some amount $P(x,y,z,t)$ of power is being transferred from the microwave field to the food at this point of time and space. There also is some heat loss due to conduction, with heat being transferred to neighbouring molecules. Mathematically the heat loss is described by the expression

$k \nabla ^2 T= k \left( \frac{\partial ^2 T(x,y,z,t)}{\partial x^2} + \frac{\partial ^2 T(x,y,z,t)}{\partial y^2}+\frac{\partial ^2 T(x,y,z,t)}{\partial z^2}\right),$

where $T(x,y,z,t)$ is the temperature at point $(x,y,z)$ and time $t$ and $\frac{\partial ^2 T(x,y,z,t)}{\partial x^2}$ is the second partial derivative of $T$ with respect to the $x$ -coordinate (similarly for $y$ as $z$ ). The constant $k$ is the thermal conductivity of the food, which measures its ability to conduct heat.

The microwave power $P$ puts energy into the food which heats it up. The heat energy is then lost through conduction. Together the heating of the microwaves and the heat loss cause the temperature $T$ at our point to change with time. We express this change in time by the partial derivative $\frac{\partial T}{\partial t},$ for which we write $T_ t$ . Multiplying $T_ t$ by the specific heat capacity $c$ of the food, that is the amount of heat needed to get the food to change temperature, balances the change in heat energy described above. We get the equation

$c T_ t =k \nabla ^2 T + P(x,y,z,t).$

(If the temperature T reaches 100 degrees, then the equation changes because we need additional energy to turn the water into steam and to then heat the steam, but we'll ignore this detail here.)

To work out the temperature $T(x,y,z,t)$ at point $(x,y,z)$ and time $t$ from this equation we have to know $P(x,y,z,t)$ . As remarked above, finding $P$ exactly is very hard, however a very good approximation can be found for ovens with either a mode-stirrer or a turntable. This approximation shows that, as long as the food you're heating is larger than 2cm in diameter, the overall the field decays exponentially as it penetrates the food.

As a result it’s possible to use a much simpler description of the electric field in the enthalpy equation than that given by a full solution of Maxwell’s equations. This takes the form

$c T_ t=k \nabla ^2 T + P e^{-x/d}.$

Here $P$ is the power of the microwave energy on the surface of the food (which is easier to calculate than $P(x,y,z,t)$ ), $x$ is the distance into the field and $d$ is a constant, called the penetration depth. It’s the length over which the microwaves start to get strongly absorbed, which is about 8mm.

This is an equation we can solve exactly, using a mathematical technique known as Fourier series analysis (find out more in the podcast Catching waves). However, it is easier to use a numerical approximation to the solution of these simplified equations. Such solutions can be found very quickly on a desktop PC. When compared against experimental values of both the temperature and the moisture content these solutions are surprisingly accurate, given the approximations that are made, and give confidence in the use of the model for further design calculations. It is the combination of mathematics, numerical methods, physical modelling and the careful use of experimental data that makes this whole approach successful. It's a typical example of the mix of ideas that have to be combined to do effective industrial applied mathematics.

Testing the model

We will now have a look at some results. In the following figures we show the results of measuring the temperature of a heated moist starchy foodstuff measured by four probes (which you can see on the photograph of the microwave oven). The first of these probes is on the outside of the food, and then they move inwards so that the fourth probe is in the centre of the food.

The blue lines show the results of lots of experiments and the red dashed line the mathematical prediction. The agreement between these two is very good. You can see that the temperature of the first probe reaches 100 degrees after about three minutes and stays at this temperature. All of the bugs will be killed there. However, the temperature of the fourth probe only reaches 100 degrees after five minutes. If you only cook your food for three minutes, then the outside will be (deceptively) nice and hot, but the inside has only got to 60 degrees and this could easily lead to a dangerous situation where the bugs are not killed. This is why you MUST stir food after heating it in a microwave cooker for a period of time, and then heat it up again, to ensure that all of the food is evenly heated.

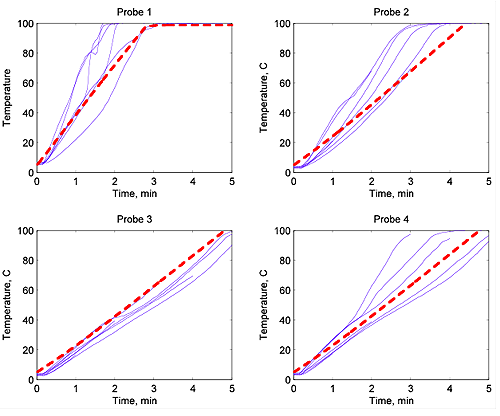
The temperature of the food over time for four probes at varying depths. The blue lines show experimental results and the red dashed lines show the mathematical predictions.

The accuracy of the above predictions are an important test of the mathematical model. Basically they show that the approximations we have made are reasonable. This then gives us confidence to use the model to do a lot of "what if" calculations to try out different designs of microwave oven and to assess them for their ability to cook safe food. It turns out that ovens with a mode stirrer are much better than those with a turntable, and those which have a chaotic frequency for the microwaves are best of all.

Conclusions

In this and the other article in the series, Eat, drink and be merry: making it go down well, I have only scratched the surface of the many ways in which maths is used in the food industry. Other applications include the use of statistical methods to ensure food quality (indeed it was Guinness that first introduced the famous t-test in statistics), the use of imaging methods to test the freshness of products such as bread and biscuits, and the use of fluid mechanics to design many sweets (you can find out more about the mathematics of imaging in my article Saving lives: the mathematics of tomography). The mathematics of heat transfer is also vitally important in the design of storage and defrosting facilities for frozen food, so that the food stays fresh and therefore safe. The food industry, and especially food safety, is an are where mathematics and mathematicians can make a major contribution.

As a final thought, if you want to see how mathematics answers the vitally important question of why the large nuts in a cereal packet are always at the top, check out the Living in a complex world website.

About the author

Chris Budd is Professor of Applied Mathematics at the University of Bath, and Chair of Mathematics for the Royal Institution. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.

He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin.