
How Euclid once ruled the world

Euclid, as depicted by Justus van Gent in the 15th century.
Geometry is obviously a very useful area of maths. We need it to measure things, to understand shapes, and to navigate through the spaces we live in.
But I'd like to argue that geometry is much more than that: it interacts with all aspects of human thought and life.
To start, let's turn to a person who is universally known as the "father of geometry": the ancient Greek mathematician Euclid. Euclid's work is the earliest example we have of a systematic approach to geometry. When you make a general statement in geometry, such as Pythagoras' theorem, you should prove this statement by deriving it from statements you're convinced are self-evident, using the rules of logic. For 2000 years Euclid's systematic approach seemed to prove truths about geometrical objects, and thereby to achieve certainty.
Euclidean rigour
Many important later thinkers believed that other subjects might come to share the certainty of geometry if only they followed the same method. René Descartes, for example, said that if we start with self-evident truths (also called axioms) and then proceed by logically deducing more and more complex truths from these, then there's nothing we couldn't come to know. The philosopher Benedict Spinoza even wrote an Ethics Demonstrated in Geometrical Order, with explicitly labelled axioms and definitions. He proclaimed to prove the existence of God, closing his proof with a QED just as mathematicians do.
In science, Isaac Newton's famous work Principia Mathematica clearly demonstrates Euclid's influence. Newton called his famous laws of motion "axioms" and deduced his law of gravitation in the form of two mathematical theorems. As Newton famously wrote, "it's the glory of geometry that from so few principles it can accomplish so much."
And here's one more example of Euclid's influence. The American Declaration of Independence is designed to inspire faith in its certainty by using the Euclidean form. Thomas Jefferson, who knew more of the mathematics of his time than any other American president, began his argument, "We hold these truths to be self-evident: that all men are created equal." There are also other self-evident truths in the document, he uses the word "prove", and the actual declaration that founded the United States is stated explicitly as the conclusion of a logical argument, beginning with a "therefore": "We, therefore ... declare, that these United Colonies are, and of right ought to be, free and independent states".
So in philosophy, theology, science, and politics, the idealised Euclidean model of reasoning has shaped conceptions of proof, truth, and certainty.
Euclid's first four postulates
- A straight line can be drawn from any point to any other point.
- A finite straight line can be extended as long as desired.
- A circle can be constructed with any point as its centre and with any length as its radius.
- All right angles are equal to one another.
Euclid's postulates
Before we look into the influence of Euclid's geometry, let's have a look at the assumptions, or postulates, he built this geometry on. The first four are shown in the box on the right. They are straightforward and nobody in their right mind would doubt them. But there is also a fifth one, called the parallel postulate:
If a straight line that falls on two straight lines makes the interior angles on the same side add up to less than two right angles, then the two straight lines, if produced indefinitely, meet on that side.
Confused? Here's a picture to understand it:
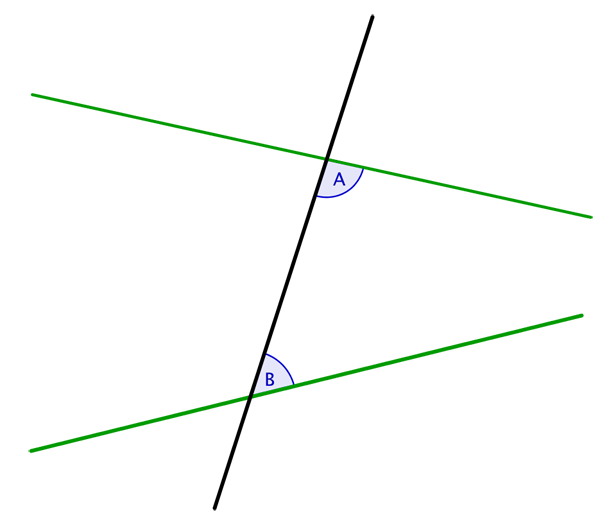
The postulate says that if angle A plus angle B add to less than two right angles, then the green lines must meet on the same side as the angles are located.
I sometimes ask my students to vote on whether this postulate is self-evident, and they overwhelmingly agree that it is not — you've got to draw a picture to even understand it. But if it is not self-evident, then maybe it should not be taken as given, but be proved from the other postulates. The Greeks tried to do this but they failed. So did medieval Islamic and Jewish mathematicians, and those in 17th- and 18th-century Europe.
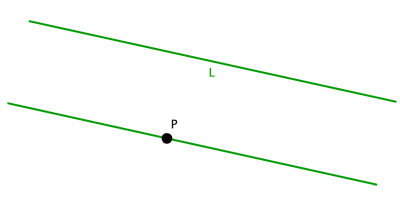
What the Greeks did manage to prove, however, is that the 5th postulate is logically equivalent to the uniqueness of parallel lines: given a line L and a point P, there is only one line through P that is parallel to L and lies in the same plane as L.
Euclid and physics
Euclid never talked about the space his geometric shapes live in, but it appears that he implicitly assumed it to be an infinite expanse that's the same in all directions and in which every point is just like every other point.
Later thinkers, especially starting in the Renaissance, talked a lot about space. And they agreed with these earlier assumptions. The idea that space should be like that comes from the principle of sufficient reason, which seems rather obvious at first glance:
For everything that is, there's a reason why it must be as it is and not otherwise.

A lever with equal weights at equal distances from the fulcrum must balance.
The principle is at least as old as Archimedes, and it allows us to explain things in the world around us. Here's an example: How do we know that a lever with equal weights at equal distances from the fulcrum must balance? Well, why not? There is no reason for the lever to go down on either side: so it must go down on neither; therefore it balances.
The greatest advocate of sufficient reason was the 17th century mathematician Gottfried Wilhelm Leibniz, who believed that God used the principle, along with the laws of logic, in making the universe. And since God made it rationally, we humans can figure it out.
A striking example of how the universe is transparent to human reason is the discovery of Newton's first Law of Motion, found fifty years before Newton independently by Descartes and Pierre Gassendi. Here's how they figured it out. The law says that a body in motion with no forces acting on it continues in a straight line at a constant speed. Why? The body continues in a straight line because it has no reason to turn away in some other direction, all the directions are the same. It goes at a constant speed because it has no reason to speed up or slow down: all the points in space are the same, so there's no reason the body should prefer being at one point to another. Similar arguments make a body at rest with no forces acting on it stay right where it is.
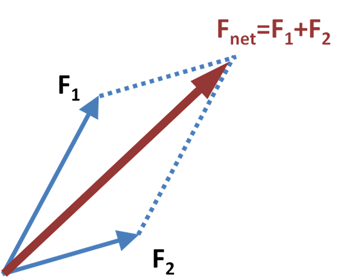
A parallelogram of forces. The two solid blue arrows represent two forces acting on a particle that sits at their tails. The lengths of the arrows represent the velocities the two forces could produce in the particle by acting on it for a unit of time, and their directions indicate the directions of the forces. The red arrow indicates the net effect of both forces acting together. Image: Brews ohare, CC BY-SA 3.0.
Sufficient reason is a powerful principle, and it seems to suggest that the space we live in is just like the space of Euclid's geometry. It's no surprise, then, that 17th and 18th century thinking was Euclidean through and through. Newton's physics, for example, implicitly relied on Euclid's 5th postulate. It needed those parallelograms of forces you might have met at school. Proving the properties of parallelograms requires Euclid's theory of parallels and thus the 5th postulate.
This is why mathematicians of the 18th century cared so much about proving the 5th postulate. It was hugely important; not just geometry, but all of science rested on it. An interesting example comes from the mathematician Joseph-Louis Lagrange: so impressed was he with the power of sufficient reason that he tried to use it to prove the 5th postulate. His argument was flawed, but it's a significant fact that such an important mathematician was willing to get up in public and link space being Euclidean with the principle of sufficient reason.
Euclid and philosophy
Philosophy was equally permeated by Euclid's ideas. A super-influential philosopher, Immanuel Kant, said that space is something that exists in our minds, and we each have the same unique "space" in our minds. And it turns out that, for Kant, this space had to be Euclidean.
To argue that we can come to know complex truths about non-material things, Kant used Euclid's proof that the sum of the angles of a triangle is two right angles. The proof uses geometrical constructions. Where do you make these constructions? Not on paper — geometry isn't about physical triangles or lines. You make them, Kant says, in the space within your mind.
It turns out that Euclid's proof requires the 5th postulate. So this theorem about the sum of the angles requires space to be Euclidean. Kant doesn't say this, but he does say there's only one space. So for Kant no alternative to Euclid seems conceivable.
Another philosopher witness to Euclidean space as truth was Voltaire. He shared the widespread 18th-century idea that universal agreement was a marker for truth. And he said, "There are no sects in geometry. One doesn't say 'I'm a Euclidean, I'm an Archimedean.' Demonstrate the truth and the whole world will be of your opinion." Mathematics exemplifies this, for Voltaire, and ethics should too! Voltaire wrote, "There is but one morality, as there is but one geometry." (And one of my students shot back, "Wrong on both points, Voltaire!" We will see why in the second part of this article.)
Euclid in art and architecture
The art and architecture of the early modern period also reflect the Euclidean idea of space. Here's the first important perspective painting of the Renaissance: the Trinity by Masaccio.

Trinity by Masaccio.
Now we are used to two-dimensional pictures that look three-dimensional because we have photography and television and iPhones and so on. In the Renaissance, they didn't have those things. So a painting like this was incredibly exciting to them. And this realistic illusion of depth in Renaissance art comes explicitly from Euclidean geometry.
It's useful to look at a medieval work of art to appreciate the difference between medieval and Renaissance art:

A piece of the Bayeux Tapestry.
These people look as big as the castle! It's wonderful art, but there is no convincing three-dimensionality.
In the Renaissance, though, we're in a different kind of space:

The ideal city attributed to Luciano Laurane or Melozzo da Forlì.
The geometry used in creating Renaissance art is literally Euclidean: results from Euclid's Elements of Geometry and from Euclid's Optics are absolutely essential to the theory of perspective used by artists, and they presuppose Euclid's 5th postulate. (To see how Euclid's geometry lets us "see" three-dimensional reality on a flat canvas, see Getting into the picture.)
Architecture also teaches us to see our world as Euclidean. Right now you are probably in a room that is full of parallel lines, walls that are everywhere equidistant and make equal right angles with the floor, all with properties Euclid proved using his 5th postulate. This is the kind of room you would design if you wanted to brainwash people to believe that space is Euclidean.
So, that's the 18th-century world, the world of sufficient reason: symmetric, balanced, based on self-evident and necessary truths, embedded in Euclidean space. We can figure it all out rationally by ourselves.
Euclid's geometry is the universally agreed upon model of perfect intellectual authority. Or is it? In the second article we will blow all of this out of the water.
About this article
This article is based on Grabiner's talk at the Ada Lovelace Symposium, which took place in December 2015 at the University of Oxford. Here's a video of the talk:
Judith V. Grabiner, Flora Sanborn Pitzer Professor of Mathematics at Pitzer College, is the author of three books and many articles (most recently The Role of Mathematics in Liberal Arts Education) on the history of mathematics. She holds a BSc in Mathematics from the University of Chicago and a PhD in the History of Science from Harvard. She is an inaugural Fellow of the American Mathematical Society, and has won both the Mathematical Association of America's Haimo Award for Distinguished Teaching of Mathematics and the MAA's Beckenbach Book Prize for A Historian Looks Back: The Calculus as Algebra and Selected Writings.