On May 30th 2024 seminar goers at Princeton University witnessed a thrilling moment. The mathematician Zhouli Xu of the University of California, LA, announced that, together with colleagues, he had sorted out the 126th dimension. Not in general, but in regards to a problem that has taunted mathematicians since the 1960s. The problem involves strange shapes and is called the Kervaire invariant problem, after the mathematician Michel Kervaire.

This year Xu visited our neighbours at the Isaac Newton institute for Mathematical Sciences (INI) in Cambridge to take part in a research programme called Equivariant homotopy theory in Context. At the INI he joined Michael Hill of the University of Minnesota, who helped to provide the previous breakthrough in 2009. 

We asked Hill and Xu to show us around the many dimensions, retracing some of the steps on the long, and sometimes arduous, journey towards a proof of the Kervaire invariant problem.

What's the nicest shape?

One way of telling the story of this intriguing problem is to start with the question "what geometric shape is the most pleasing"? It's a matter of taste and personal preference, but a strong contender is the sphere. It is perfect in its roundness, never-ending, and self-contained.  

It's an ideal shape that is easy to describe. A sphere consists of all the points that are a fixed distance r away from a given centre point. Once you know the centre point and the number r (the radius) you know everything there is to know about the sphere. It's a perfect balance of simplicity and perfection. "The sphere is a very beautiful object," says Xu. "If you are looking for [an object that is finite in extent], the sphere is the first example you get.

Topology and the importance of holes

Given this special status of the sphere, a natural question to ask is this: given any other shape, how different is it from a sphere? Golf balls and oranges are not perfect spheres. They have dimples and bulges. It would be unfair, however, to say that the shapes they form are fundamentally un-spherical.

The mathematical field of topology helps us capture this. In topology two shapes that can be deformed into each other without cutting or glueing are considered equivalent. In this more lenient way of looking at things, golf balls and oranges are equivalent to spheres.

The sphere is a surface. While its natural habitat is the three-dimensional Euclidean space we learn about at school, it is itself a two-dimensional shape. There are of course many other surfaces too, in fact there are infinitely many. The screen of your phone or laptop defines a surface, and so does the doughnut you're about to have with your coffee, which sits in a cup that also defines a surface. 

There is in fact an infinite zoo of surfaces. And when mathematicians encounter such an infinity of objects, they have an urge to classify them. "The power of a classification theorem is that it gives you a complete list," says Xu. "It's like having a bunch of baskets. [Given a specific object you have a way of deciding] which basked it should go into."

In the world of topology the road to classification is given by holes. Surfaces that are topologically equivalent to a sphere can't have any holes: if they did, then you'd have to glue these holes shut to get a sphere and you are not allowed to do that. This is why a doughnut, technically known as a torus, is not equivalent to a sphere. It is, however, equivalent to a coffee cup because the cup also has one hole.

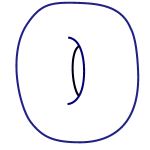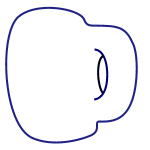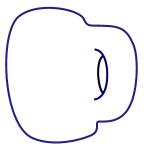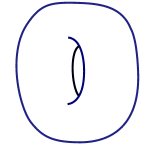
This works more generally for other surfaces too. Suppose you are looking at a surface which is of a similar nature to both the sphere and the torus in that it is closed. This means, firstly, that it has no edge you could fall over when walking around on it. That's the case for the sphere and the torus, but not for a disc which does have a clearly defined boundary. Being closed also means that your surface is finite in the sense that you could construct it by sewing together a finite number of patches (this property is also known as being compact). Again that's the case for the sphere and the torus, but not for the plane which goes on infinitely in all directions so you'd need infinitely many patches. 

Finally suppose the surface you are looking at is orientable, which means that it has a clearly defined inside and outside. This is true for the sphere and the torus, but not for the Möbius strip which consists of a single side.

It turns out that any closed and orientable surface is completely determined, topologically,  by the number of holes it has:  if it has no holes then it is topologically equivalent to a sphere, if it has one hole then it is topologically equivalent to a torus, if it has two holes then it is topologically equivalent to a torus with two holes, etc. Once you have determined the number of holes of your surface (which is also known as the genus of the surface)  you know which topological class it belongs to — it's a neat hierarchy of holes.

 The number of holes of a surface is what mathematicians call an invariant. It does not change (vary) when you transform the surface in the ways allowed by topology, without cutting or gluing. Generally in maths invariants can be a useful tool when it comes to classifying objects. All objects for which the invariant takes the same value go in the same basket. In our example, we have a basket for surfaces with no holes, a basket with surfaces with one hole, a basket for two holes, and so on.

Going back to our question of which surfaces we might consider being "close to" or "nearly" a sphere we now have a possible answer. They are the ones in the first basket:  closed, orientable surfaces that have no holes.

Adding dimensions 

As the beginning of this article suggests, the really interesting action happens when we go up in dimension. It's impossible to visualise shapes in higher dimensions — our brains simply are't designed to do this. However, it is perfectly possible to define higher dimensions and shapes that live within them mathematically. If you have the mathematical tools you don't need to be able to see an object to work with it.

The ordinary sphere we know and love is known as the 2-sphere because it is a two-dimensional object. For each dimension n, where n can be any integer from 3 upwards, there is an analogue of the 2-sphere called the n-sphere. And just as the 2-sphere lives in a surrounding three-dimensional space you can think of the n-sphere as living in a surrounding n+1-dimensional space.

For each dimension n there are also shapes called n-manifolds. For our purposes these are the analogue of surfaces (see here for a more precise definition of a manifold). They are n-dimensional shapes that come with maps that help us understand them. To find out more about higher dimensions see this article and to find out more about higher dimensional spheres in particular see this article. 

The Poincaré conjecture

You can now ask the same question we asked above. Which n-dimensional manifolds are topologically equivalent to an n-sphere? For the 3-dimensional manifolds, this question triggered a mathematical quest that lasted a hundred years. Inspired by the result for the ordinary 2-sphere, the French mathematician Henri Poincaré conjectured, in 1904, that exactly those 3-dimensional manifolds that are closed and have no holes (where the property of "having no holes" is suitably defined) are topologically equivalent to the 3-sphere.  See here to find out more about the Poincaré conjecture.

Since this is in direct analogy to what happens in the dimension below, which we can still visualise, you might think the result should have been easy to prove. Alas, it was not. Much of 20th century effort in algebraic topology was focussed on proving the Poincaré conjecture. Success finally arrived in the early 2000s when the Russian mathematician Grigory Perelman published three papers which proved the conjecture (in fact he proved a more general result, called Thurston's geometrisation conjecture, named after the mathematician Bill Thurston). Perelman was awarded a Fields Medal, one of the most important prizes in mathematics, for his work in 2006, but refused to accept it.

Since the Poincaré conjecture was so hard to prove for the 3-sphere, you'd think that higher dimensions would pose even more of a problem. But oddly, this wasn't the case. Generalised versions of the Poincaré conjecture for spheres of dimensions 4 and higher were proved quite a while before Perelman came up with his proof for the 3-sphere — in the 1960s for spheres of dimensions 5 and above and in the 1980s for  spheres of dimension 4. Three Fields medals were awarded for the effort: to John Milnor, Steve Smale, and Michael Freedman. (You can read a brief history of the generalised Poincaré conjecture on Wikipedia.)

Having sorted out the closest topological relatives of the sphere in any dimension we might now go and look for slightly more distant relatives — and that's what the Kervaire invariant problem is all about. Find out more on the next page...

About this article

Michael Hill is Ordway Professor at the University of Minnesota.

Zhouli Xu is a Professor in the Department of Mathematics at the University of California, LA.

Marianne Freiberger, Editor of Plus, interviewed Hill and Xu in April and June 2025.

This content forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.

The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.