Maths in a minute: The binomial distribution

In our brief introduction to probability distributions we talked about rolling dice, so let's stick with that example. Imagine I roll a die three times and each time you try and guess what the outcome will be. What's the probability of you guessing exactly k rolls right, where k is 0, 1, 2 or 3?

More generally, imagine you perform an experiment (eg roll a die) $N$ times, and each time the result can be success or failure. What's the probability you get exactly $k$ successes, where $k$ can be any integer from $0$ to $N$?

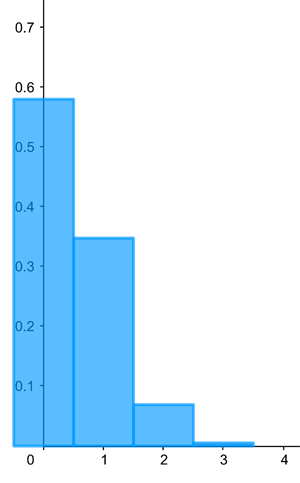
In our example, as long as the die is fair, you have a probability of $p=1/6$ of guessing right. Since the probability of three independent events (ie guessing correctly) is the product of the individual probabilities, your probability of three correct guesses is $$P(Correct = 3) = 1/6 \times 1/6 \times 1/6 = (1/6)^3\approx 0.005$$ Your probability of guessing wrong is $1-p=1-1/6=5/6$. By the same reasoning as above, the probability of getting no guess right is $$P(Correct = 0) = 5/6 \times 5/6 \times 5/6 = (5/6)^3\approx 0.579.$$

What about the probability of guessing one roll right, so $k=1$? There are three ways in which this could happen:

• You get the 1st roll right and the other two wrong
• You get the 2nd roll right and the other two wrong
• You get the 3rd roll right and the other two wrong

Since each involves one correct and two incorrect guesses, the probability of each of the three scenarios is $1/6 \times (5/6)^2.$ And since the probability of any one of three events occurring is the sum of the individual probabilities, we have that the probability of getting exactly one guess right is $$P(Correct=1)=3\times 1/6 \times (5/6)^2 \approx 0.347. $$ Finally, we look at the probability of two correct guesses. Again this can happen in three ways (we leave it up to you to work these out). Each individual way has a probability of $(1/6)^2\times 5/6$, so the overall probability is $$P(Correct=2)=3\times (1/6)^2 \times 5/6 \approx 0.069. $$

Here's the histogram displaying the distribution.

Now let's look at the general set-up. You're doing $N$ experiments that can each end in success or failure, and you're asking for the probability that there are exactly $k$ successes among the $N$ experiments. Write $p$ for the probability of success so $1-p$ is the probability of failure. By the same reasoning as above, a particular sequence of $k$ successes and $N-k$ failures has probability $$p^k(1-p)^{N-k}.$$ But, also as above, such a sequence can occur in several ways, each way defined by how the successes are sprinkled in among the failures. It turns out that the number of ways you can sprinkle $k$ objects in among a sequence of $N$ objects, denoted by ${N\choose k}$, is given by $${N\choose k} = \frac{n!}{k!(n-k)!}.$$ Here the notation $i!$, where $i$ is a positive integer, stands for $$i!=i\times (i-1)\times (i-2)\times ... \times 2 \times 1.$$ (and $0!$ is defined to equal 1). We now have a neat way of writing the probability of $k$ successes: $$P(Correct=k) = {N\choose k}p^k(1-p)^{N-k}.$$ That's the binomial distribution.

The mean of this distribution, also known as the expectation is $Np.$ So in our example above where $N=3$ and $p=1/6$ the mean is $$Np=3/6=1/2.$$ Loosely speaking, this means that if we played our game of guessing three rolls lots and lots of times, then on average you could expect to get half a roll per game right. Or, to phrase it in a way that uses whole numbers on average you could expect to get one roll in two games right.

The variance of the binomial distribution, which measures how spread out the probabilities are, is $$Np(1-p).$$ So in our example above it is $$Np(1-p)=\frac{3}{6}\times \frac{5}{6}=\frac{5}{12}.$$

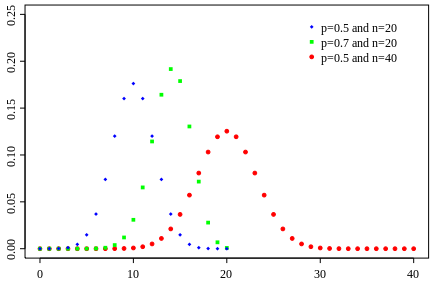
The shape of the binomial distribution depends on the value of the mean and the number of experiments. Here are some more examples: