Think of a geometric shape, any shape. Lines, circles and triangles come to mind. Going up a dimension you get surfaces. The perfect sphere is one example. Others are a flat piece of paper, the surface of a doughnut, or perhaps something more exotic as in the image below.

A sphere, a doughnut (technically called a torus), and the surface given by the equation z=x³+y³+1.

How many different surfaces are there and what do they all look like? That question seems impossible to answer. But mathematicians are good at classification, and they have a way of dealing with the multitude. As we have reported previously, there's a neat way of classifying (certain types of) surfaces when you let go of notions like distance and angle and allow yourself to deform surfaces by squeezing and stretching, but without cutting or gluing them.

If you consider two surfaces to be equivalent if you can deform one into the other in this way, then many surfaces that readily spring to mind are equivalent to one of the following: the sphere, the doughnut, the doughnut with two holes, the doughnut with three holes, and so on. Technically any surface that is closed (it has no edge and can be painted with a finite amount of paint), orientable  (it has an inside and an outside), and consists of a single connected piece falls into one of these classes.

A sphere, a torus, a surface with two holes, and a surface with three holes.

The area of maths which studies shapes allowing for deformations in this way is called topology — every surface of the type mentioned above is topologically equivalent to the sphere or a doughnut with some number of holes. This means, for example, that a very thin doughnut is topologically equivalent to a very fat doughnut because one can be deformed into the other. What matters is only the number of holes.

Allowing deformations is, in some ways, quite a natural thing to do. In ordinary life, we consider golf balls and oranges to be spherical, even though their bumps and dimples mean they aren't perfect spheres. Sometimes, however, you want to be a little more rigid. When it comes to the inner tubes on your bicycle, for example, it really does matter if they are thin or fat.

So what if we put a limit to how much things can be deformed, for example by retaining the notion of an angle? Can we still say something about what kind of different surfaces there are in this case? The answer is yes — and it takes us into an area of mathematics where geometry meets algebra, and where even theoretical physics has a hand in the game. Generalisations of this area are the subject of lots of active research and have recently been explored by a research programme at the Isaac Newton Institute for Mathematical Sciences in Cambridge.

In this series of three articles we'll give an intuitive introduction to how mathematicians go about classifying certain types of surfaces to give you an idea of the elegant picture they have constructed. But we have also included links to more technical explanations for those who'd like to learn more.

Surfaces à la Riemann

When we talk about surfaces we mean objects that locally look like the flat plane we're used to from school geometry. A sphere is like that, as we experience every day: we live on a roughly spherical surface, but to us, who are small compared to the surface, it seems flat. Objects that locally look like the plane are also called two-dimensional manifolds. Given a small enough patch on such a manifold, there's a way of mapping it onto a region of the plane: by mapping it we mean that for every point on one patch there's exactly one point on the region of the plane and vice versa. This is exactly what happens with maps of regions of the Earth.

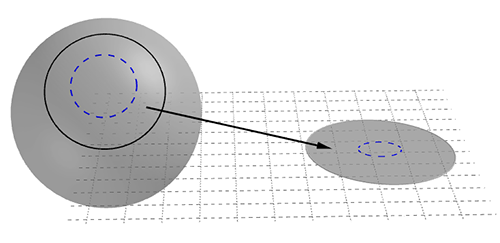
The region inside the black curve on the sphere is mapped to a region on the plane. The blue dashed circle on the sphere is taken by this mapping to the blue dashed curve on the plane.

Each individual mapping from a patch of surface to the region of the plane is a mathematical function also called a chart. (Technically, to define a manifold, we require the charts to be homeomorphisms.) Given charts defined on a collection of overlapping patches that cover the entire surface we get what is called an atlas. If you printed the maps of all the patches on separate pages of a book, you'd get the analogue of those old-fashioned books people used to use to map out the Earth before there was Google maps, which are of course also called atlases.

Note that an atlas describes a surface entirely through maps which live in the plane — we haven't needed to make reference to the surrounding space a surface might sit in, even though that's what we do when we visualise it on the page or in our mind's eye.

This is neat, but it means we haven't got a way of measuring angles on our surface, as we can't borrow the notion of an angle from a surrounding space. A Riemann surface, named after the 19th century mathematician Bernhard Riemann, is a two-dimensional orientable manifold that comes with a little more structure, so that we do have a way of measuring angles. The structure comes from what are called Riemannian metrics, ingenious ways developed by Riemann of measuring distances and angles on an object from within, without having to first place it into a surrounding space. (Interestingly, generalisations of these metrics are a crucial ingredient of Einstein's general theory of relativity, but that's another story.)

When are two Riemann surfaces the same?

We can now be more discerning about when we consider two Riemann surfaces to be the same. We said that two surfaces are topologically equivalent if one can be turned into the other by squeezing or stretching but without cutting or gluing. We say that two Riemann surfaces are isomorphic (a fancy way of saying they are the same in some way) if one can be deformed into each other, but without distorting angles. (Technically we require the two surfaces to be conformally equivalent, a relationship which is also sometimes called biholomorphic.) Two surfaces can be topologically equivalent but not isomorphic because the deformation it would take to turn one into the other may distort angles. This could happen, for example, when a fat doughnut is stretched to give a thin doughnut.

There's another thing we should say about Riemann surfaces. The plane can also be regarded as the collection of all complex numbers. These are an extension of the real numbers and they're inherently more two-dimensional — while all the real numbers combine to form a line, all the complex numbers combine to form a plane, called the complex plane. Topologically this is just the ordinary plane, but the complex numbers give it a little more mathematical structure, which constrains the nature of mathematical functions we can define on it.

The real numbers all merge together to form a line, essentially an infinitely long ruler.

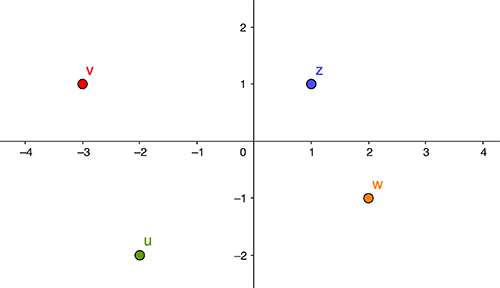
A complex number is defined by two real numbers, which you can interpret as coordinates specifying a point in the plane. All the complex numbers taken together give you the entire plane. The complex numbers shown here are z=1+i, w=2-i, u=-2-2i, v=-3+i. Find out more here.

You don't really need to understand the complex plane to understand this article. Suffice to say that a Riemann surface is a surface that locally looks like this complex plane. The structure that exists on a Riemann surface, which enables us to define angles, is also called a complex structure.

We're now in a position to think about what types of different Riemann surfaces there are. To find out, see the next part of this article.

About this article

Ruadhaí Dervan (second from left) and Victoria Hoskins (third from left) together with two other organisers of the research programme, Frances Kirwan (left) and Gergely Berczi (right).

This article was inspired by the research programme New equivariant methods in algebraic and differential geometry which took place at the Isaac Newton Institute for Mathematical Sciences in Cambridge between January and June 2024. It was produced in collaboration with Ruadhaí Dervan and Victoria Hoskins, who co-organised the programme.

Ruadhaí Dervan is a Senior Lecturer at the University of Glasgow, where he researches the geometry of higher-dimensional spaces.

Victoria Hoskins is an assistant professor at Radboud University Nijmegen, where she researches symmetries and moduli spaces in algebraic geometry.

Marianne Freiberger is Editor of Plus and would like to thank Ruadhaí and Victoria for all their help with this article.

This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI). The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. The Newton Gateway is the impact initiative of the INI, which engages with users of mathematics. You can find all the content from the collaboration here.