This article is about understanding what types of different Riemann surfaces there are. To find out what a Riemann surface is, see the previous article.

What different Riemann surfaces are there?

Now that we have an idea of what a Riemann surface is, and what it means for two Riemann surfaces to be isomorphic, we can ask what we can say about all the different kinds of Riemann surfaces there are, where "different" means not isomorphic.

Since holes played such an important part earlier let's first look at Riemann surfaces with no holes. Let's also agree to only consider Riemann surfaces that don't go on infinitely in any direction and don't have a definite edge — a sphere would qualify here, but the entire plane wouldn't (it goes on infinitely in all directions) and neither would a disc (it has an edge). Technically, we only consider closed Riemann surfaces.

We said in the previous article that every closed, orientable and connected surface without holes is topologically equivalent to the sphere. Something similar is true for Riemann surfaces: every compact Riemann surface without holes is isomorphic to something called the Riemann sphere. This comes from adding a point at infinity to the complex plane (find out more here) but you can think of it as the ordinary sphere, equipped with some extra structure that comes from the complex plane. Crucially, this means that all compact Riemann surfaces without holes are isomorphic to each other.

So let's move on to compact Riemann surfaces with one hole. In topology a thin donut is equivalent to a fat one. It turns out that this is not the case for the more rigid notion of isomorphism between Riemann surfaces. There are Riemann doughnuts that aren't isomorphic to each other, even though they are topologically equivalent.

But how can we distinguish between different Riemann doughnuts, that is, Riemann doughnuts that are not isomorphic to each other? To answer this question we will explore a beautiful way of characterising the essence of a Riemann doughnut by flattening it out and "unfolding" it.

Unfolding the doughnut 

First, let's switch to using the correct technical term for a doughnut: a closed surface with one hole is known in mathematics as a torus. Straying slightly from convention, we will call a torus which is also a Riemann surface a Riemann torus (technically it's called a Riemann surface of genus 1).

Let's also make the crucial observation that you can create a torus from a rectangle. First glue two opposite sides of the rectangle to get a cylinder. Then bend the cylinder around and glue the two circular edges to get a torus.

A torus can be made from a rectangle. Animated gif by Lucas Vieira, in public domain.

This gives us a way of relating our home-made torus to the (complex) plane: simply place the rectangle in the plane so that its bottom left corner coincides with the origin of the coordinate system on the plane — that's the point with coordinates (0,0) using the standard Cartesian coordinate system, or equivalently, the complex number 0.

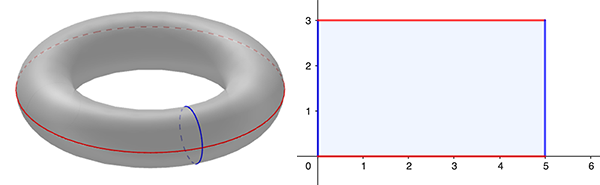
Cutting the torus along the red and blue lines gives a rectangle, which can be placed in a standard Cartesian coordinate system as shown.

Now notice that you can wind around the hole of the torus in two ways. If the torus is placed as in the image above (left), there's a horizontal way (for example along the red curve) and a vertical way (for example along the blue curve). This is what topologically differentiates the torus from the sphere (there's no hole to wind around) and a torus with more holes (where a loop has multiple choices of a hole to wind around, see here to find out more).

A complicated path on the torus could wind around the hole multiple times, this way or that, in a particular configuration. If we cut the torus open again to form the rectangle then this path will correspond to a criss-cross pattern on the rectangle, consisting of lots of bits of path. Whenever the path on the torus traverses one of the cut lines, the path on the rectangle stops at a side of the rectangle (which comes from the cut) and then appears again at the corresponding point on the opposite side.

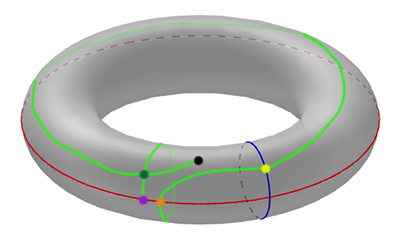
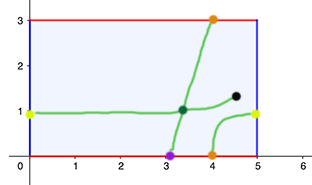
The green path on the torus translates to a collection of paths on the rectangle.

We can make the picture much clearer by placing lots of copies of our original rectangle on the plane so that sides corresponding to the same cut line up. This creates a tiling of the plane by rectangles.

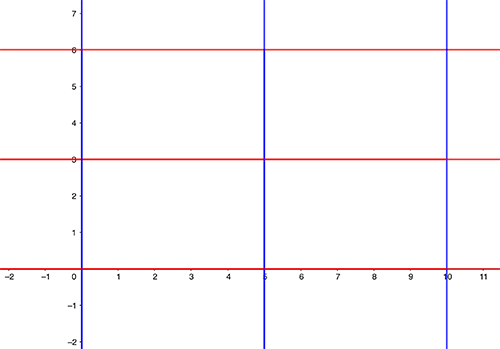
A tiling of the plane by rectangles.

Each copy of the rectangle can be made into the torus in the same way as the original one, by gluing opposite sides.The multiplicity of rectangles represents the multiplicity of ways a path can wind around the torus. We can trace the path starting in our original rectangle until we hit a side (when the path of the torus crosses a cut line). Rather than continuing our path on the opposite side of the original rectangle, we simply continue across the side into a neighbouring, identical, copy of the rectangle. When the path on the torus crosses a cut line a second time, we again continue on into a neighbouring copy. And so on.

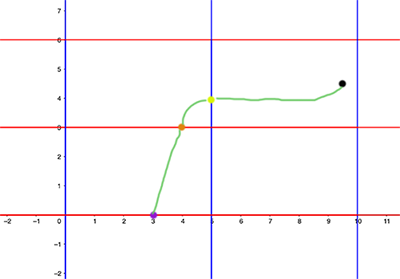
The green path depicted on a tiling by rectangles which each represent the original torus.

A path on the torus winding around the hole multiple times in a particular fashion now corresponds to a continuous path through the tiling visiting a collection of rectangles in a particular order, and vice versa. The tiling represents, in a very clear way, the totality of all the ways you can repeatedly wind around the torus' one hole — which captures its topological essence. At the same time, it links our torus to the complex plane.

Technically, the corner points of all our rectangles from what is called a lattice (a grid of points) in the plane. The torus is what is called the quotient of the plane by this lattice. Loosely speaking, by quotienting the plane we mean that all the different copies of the rectangle are stacked back on top of each other and merged down, and then the sides of the rectangle are glued back together. (Technically, what we have is a quotient by a group action, where the group is formed by the translations that take the rectangles to each other).

It turns out that any Riemann torus can be thought of as the complex plane quotiented by a lattice. The lattice does not have to come from a rectangle, as in our example, it can also come from a parallelogram (technically the lattice is defined as $\mathbb{Z}z \oplus \mathbb{Z}w$, where $z$ and $w$ are complex numbers).

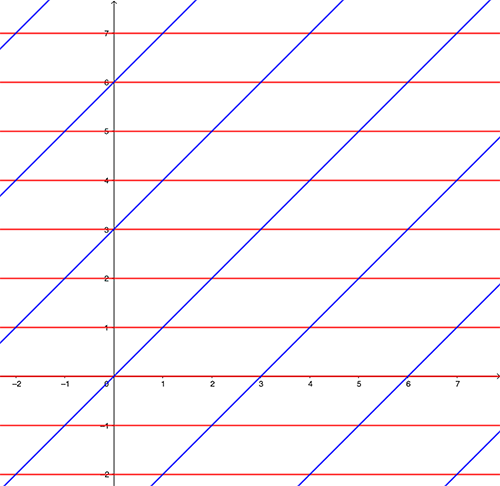
A tiling of the plane by parallelograms. If you quotient the plane by the lattice formed by the corner points of the parallelograms you get a torus.

When are two Riemann tori the same?

Our way of thinking of a Riemann torus as related to a lattice now gives us a convenient way of seeing what it means for two Riemann tori to be isomorphic. We do this at the level of the lattices that are linked to the tori.

For our purposes, a lattice is a grid of points in the complex plane. Such a grid is given by two arrows, each with a particular direction of length (these are given by the two complex numbers $z$ and $w$ in the definition of a lattice above).

The origin is one point in our lattice. All other lattice points can be reached by following any combination of the two arrows and their exact opposites (which point in the opposite directions but have the same length).

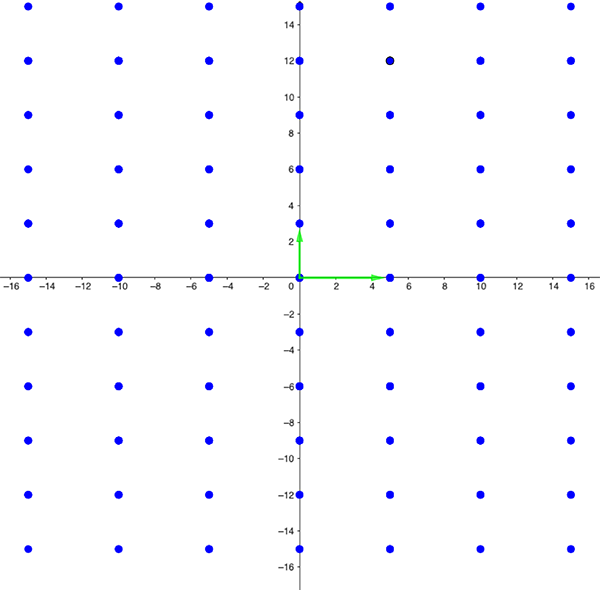
Lattice 1. All points can be reached by following a combination of the green arrows and their exact opposites.

We say that two lattices are isomorphic if one can be turned into the other by rotating and/or scaling by a particular factor r. Scaling by a factor of r means that distances are being stretched away from the origin by the factor r (or shrunk towards it if r is less than 1). It makes sense to consider two lattices that are related in this way as being the same. A rotation doesn't change how the points in the lattice are placed in relation to each other. Scaling can be thought of as zooming in or out of the picture. (Technically, two lattices are isomorphic if and only if one is a scalar multiple of the other, where the scalar is a non-zero complex number.)

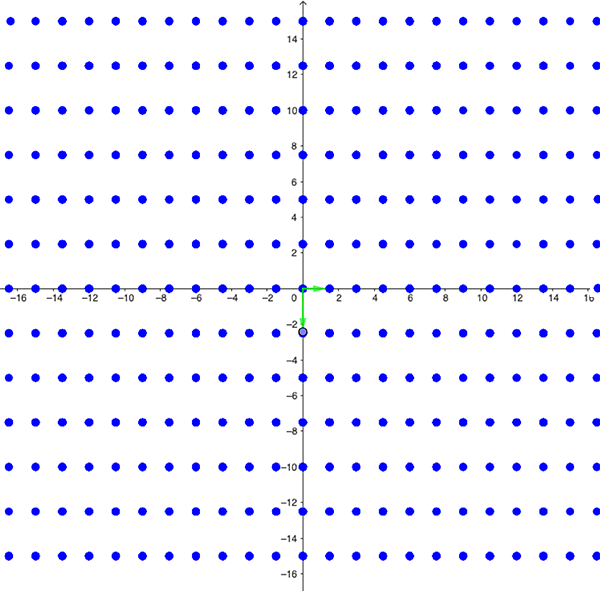
Lattice 2 can be made from lattice 1 using a clockwise rotation through 90 degrees and scaling by a factor of 1/2. The two lattices are isomorphic.

Here is the important result regarding Riemann tori: it turns out that two Riemann tori are isomorphic if and only if the lattices that define them are isomorphic. In other words, if you can deform two Riemann tori into each other without distorting angles, then their corresponding lattices can be turned into each other using just a rotation and scaling — and vice versa.

We're now ready to return to our original quest: to understand the entire universe of Riemann tori. Find out more in the next article.

About this article

Ruadhaí Dervan (second from left) and Victoria Hoskins (third from left) together with two other organisers of the research programme, Frances Kirwan (left) and Gergely Berczi (right).

This article was inspired by the research programme New equivariant methods in algebraic and differential geometry which took place at the Isaac Newton Institute for Mathematical Sciences in Cambridge between January and June 2024. It was produced in collaboration with Ruadhaí Dervan and Victoria Hoskins, who co-organised the programme.

Ruadhaí Dervan is a Senior Lecturer at the University of Glasgow, where he researches the geometry of higher-dimensional spaces.

Victoria Hoskins is an assistant professor at Radboud University Nijmegen, where she researches symmetries and moduli spaces in algebraic geometry.

Marianne Freiberger is Editor of Plus and would like to thank Ruadhaí and Victoria for all their help with this article.

This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI). The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. The Newton Gateway is the impact initiative of the INI, which engages with users of mathematics. You can find all the content from the collaboration here.