Over recent years mathematical models have nudged their way towards the mainstream. Many people have heard of weather and climate models, they may be aware that models are used in the financial world, or that they helped inform policy decisions during the COVID-19 pandemic.

To devise a mathematical model you obviously need to know your mathematics, and you also need expertise in the processes that are being modelled. What is less well-known, however, is that modelling goes hand-in-hand with the art of coding. That's because most real-world models are so complex, computers are needed to tease out usable answers.

One person pursuing this art is Alison Hale, research software engineer at the JUNIPER network of epidemiologists. Members of the JUNIPER network build mathematical models of how infectious diseases spread. In her role Hale offers support in writing the computer programs that generate the models' outputs, transforming the models into reliable, usable and reusable tools. This bridges the gap between computer science and mathematical modelling by applying principles from software engineering to solve research problems within epidemic modelling.

Because the coding aspect of modelling is rarely talked about, we asked Hale to explain just why it's so essential.

Difficult equations…

Mathematical models involve equations that need to be solved. Usually the equations describe how something is changing over time: they are differential equations.

For a rare few of these equations, the ones you tend to learn about in an introductory course, there's a neat formula giving you the solution. For the vast majority, however, no such formula is known. In that case, algorithms are used to find solutions. Computing these algorithms is a lengthy business — if you want solutions that are sufficiently accurate for real-world use, computers are the only option. (See here for a simple example of a technique for approximating solutions to a certain type of differential equation, including a link to some code.)

"There are more differential equations that you can't solve by hand than there are differential equations that you can solve by hand," says Hale. In the modelling of infectious diseases, the area Hale currently works in, anything more complex than the simplest of models requires computers.

Another notorious example are the Navier-Stokes equations which describe the behaviour of fluids, such as the flow of air around an aircraft wing or processes within the Earth's atmosphere or oceans. These equations are so hard to solve that a whole field of maths, called computational fluid dynamics, has been developed to find approximate solutions. One area where the Navier-Stokes equations are used is weather forecasting, which requires, not just computers, but supercomputers.

…and elusive parameters

Another problem is that mathematical models involve parameters, numbers that pertain to the particular situation you're applying the model to. In some cases the parameters describe quantities you can quite easily measure. That's the case for temperature and pressure, for example, which are important parameters in weather modelling.

In other situations parameter values aren't so easy to come by. An example is modelling the spread of a disease through a population, where a model might be designed to estimate the number of infected people after a given length of time. Model parameters here might include the rate at which people become infected or the proportion of infected people that show no symptoms, which are challenging to measure directly. (See here for an example of a simple disease model — the SIR model.)

One way of dealing with this problem, which can be used in practice, is to run your model many times, perhaps a thousand times or more, each time with different values for the parameters. You then compare the outputs of your model (e.g. the predicted number of infected people) with data from real life. The set of values that gives the closest match to real-life data then gives you a good estimate for the parameters (there are many statistically rigorous methods for doing this kind of estimation).

This means that you need to solve your model, not just once, but potentially thousands of times, before you can even employ it. Even if the central equation (or equations) of the model are simple, this is not something you'd be able to do by hand.

Why off the shelf won't do

All this means that computers are essential in modelling, but it doesn't necessarily imply a need for coding. We all use computers every day but few of us know how to write programs. Instead we use off-the-shelf products software engineers have designed for us.

Such off-the-shelf products also exist in the world of equation solving, provided by mathematical software packages. The problem with mathematical models is that they're typically too complex and bespoke to simply give to a software package to solve. In infectious disease modelling, for example, you might want to describe several different processes — such as infection, recovery, and vaccination — for different groups of people inside the same model, each needing its own equation. To have such a model solved by a software package you do still need a level of coding, and sometimes a package may not be able to accommodate a model at all.

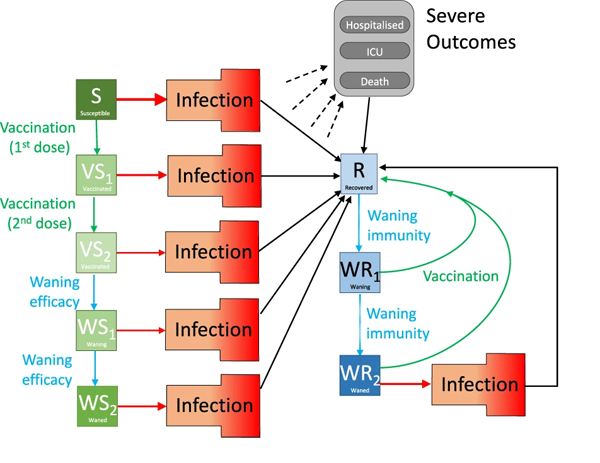
"There are some packages which come ready-made but they are very specific to particular equations," says Hale. "You still need to be able to put those lego pieces together to make a house in the end. As a modeller you can soon fall outside of a dedicated package designed for a particular class of problems."

Models also tend to be highly specific, not only to the disease in question, but also to the questions that need answering — a model designed to explore the effect of a lockdown will be very different from one designed to explore the effect of vaccination. Other areas where modelling is applied require similarly bespoke approaches. Off-the-shelf solutions, even ones specific to a particular area of science, are rarely an option.

The black art of testing

Once a model has been devised and turned into code, a particularly tricky aspect of coding begins: checking for errors. Given that models are used in safety-critical applications, such as the design of planes, or to inform policy decisions that affect us all, the importance of testing can't be stressed enough.

"Testing is a bit of a black art and it's something that I think we need to spend a lot more time doing," says Hale. "There are external tests, sanity checks to make sure that the whole thing is producing something sensible," says Hale. "For example in disease modelling, if you start off with three infected individuals and your model says that in three days you'll have 10 million then something is probably wrong."

Such sanity checks can also be applied to individual elements of a model to catch internal errors that don't necessarily raise a red flag in the overall output. For example, if there are variables in the model that should never become negative (e.g. the number of people infected with a disease) then the code should contain an instruction to stop and produce an error message should this happen at any point during its internal calculations — even if the calculations haven't yet finished.

"Being able to write some of those contextual tests, that's where you might struggle if you don't have a deep enough knowledge of both mathematics and the area the model applies to," says Hale.

Culture shift

This means that coding is an integral part of modelling. You can't outsource or automate it. At the same time, it's a tall order to require all this coding expertise of mathematical modellers, who already need to possess an enormous amount of expertise, both in maths and in the domain that's being modelled, and typically don't receive a lot of computer training.

A lack of training may also mean that modellers fall short of software engineering standards of practice, producing code that others will find hard to understand and use, or to find in the first place. "It's important to make your code accessible to others and to properly document it so that everybody knows what it is you've done," says Hale. "Otherwise there's a real danger that a model becomes a black box." When this happens others will find it hard to build on your work or even just to reproduce it — reproducibility being, after all, one of the main pillars of scientific practice.

A software engineer embedded in a research community, as Hale is in the JUNIPER network, is therefore an enormous, even essential help. “Having Hale working alongside the mathematical modellers, embedded within the research work, is critical to ensure we can trust the outputs of our models and ultimately improve coding practices within the modelling community," says Ciara Dangerfield, Senior Scientific Programme Manager at JUNIPER.

However, having a software engineer embedded in this way is not common practice — research budgets are tight and modellers, as well as funders, don't always recognise the importance of software engineering.

Hale argues for a culture change in this respect. "We need to think of asking for funding for software engineering so it becomes part of the process." A full-time software engineer is expensive, of course, but other options include sharing their time over multiple research groups, as is the case for the JUNIPER network, or paying for thorough training for modellers.

This, Hale points out, would merely put mathematical modelling on a par with other subjects. "If we were going to fund a project that has to happen in a lab, something a biologist or chemist might do, we wouldn't try and do that without having the lab equipment and the staff."

About this article

Alison Hale is a Research Fellow in the Mathematics Institute at the University of Warwick, in this role she serves as the Research Software Engineer for the JUNIPER Partnership. She has a broad background gained in industry and business, as well as a PhD in mathematical physics.

Marianne Freiberger, Editor of Plus, interviewed Hale in December 2024.

This article is part of our collaboration with JUNIPER, the Joint UNIversities Pandemic and Epidemiological Research network. JUNIPER is a collaborative network of researchers from across the UK who work at the interface between mathematical modelling, infectious disease control and public health policy. You can see more content produced with JUNIPER here.