
Understanding uncertainty: The many ways of spinning risk

Yummy?
In this article we explore how risks can be spun to look bigger or smaller simply by changing the way evidence is communicated. Research has shown that people's perception of risk is vulnerable to this type of manipulation, and it becomes particularly relevant where health issues are concerned. Medical treatments can be presented as miracle cures or as completely useless, and life style changes can be made to look imperative, or not worth bothering with, all by changing the way risk is presented.
Absolute or relative?
A good example to look at is the "bacon sandwich debate". A major report estimated that there was a 20% increased risk of bowel cancer if you eat 50g of processed meat every day — that's a large bacon sandwich. The Sun came up with the beautiful headline "Careless pork costs lives!", and other papers too seized on this result. The risk presented here is a relative risk and can sound quite frightening. For an average person, the chance of getting bowel cancer at some point in their life is around 5%. Now 20% of 5% is 1%, so a relative increase of 20% translates to a lifetime risk of 6%, or an increase of 1% in absolute risk, which now does not sound so bad.
Yet another way to think of this is to consider how many people would need to eat large bacon sandwiches all their life in order to lead to one extra case of bowel cancer. This final quantity is known as the number needed to treat (NNT), although in this context it would perhaps better be called the number needed to eat. To find the NNT, simply express the two risks (with and without whatever you are interested in) as decimals, subtract the smaller from the larger and invert: in this case we get 1/(0.06 - 0.05) = 100 — a hundred people would need to eat large bacon sandwiches all their lives in order for one extra case of bowel cancer to occur. Now the risk does not seem at all remarkable.
It has been shown in experiments that these different ways of expressing risk differences can carry very different messages to people. One of the most misleading, but rather common, tricks is to use relative risks when talking about the benefits of a treatment, for example to say that "Women taking tamoxifen had about 49% fewer diagnoses of breast cancer", while potential harms are given in absolute risks: "The annual rate of uterine cancer in the tamoxifen arm was 30 per 10,000 compared to 8 per 10,000 in the placebo arm". This tends to exaggerate the benefits, minimise the harms, and in any case make it hard to compare them. This way of presenting risk is known as mismatched framing, and was found in a third of studies published in the British Medical Journal.
Population or parallel universes?
We can also spin the risk by changing the number we use to describe it. First, we can think of getting bowel cancer as an event that is similar to the flip of a coin or a throw of dice, unpredictable but with some physical basis. This creates an image of life as a gamble with the outcome determined by some invisible mechanism over which we have no control. A very popular alternative, used by most people trying to communicate risk, is to think of the frequency of the event expected to occur in a population of similar individuals, that is a group of "people like you", some of whom will get bowel cancer and others who won't. A disadvantage of this analogy is that people may feel that the risk in question has nothing to do with them: who's to say that a group of 100 people "just like you" really exists, and even if it does, you may well think that you are going to be one of the lucky ones.
To reduce the danger of people thinking of the problem as belonging to others, risk communicators sometimes talk about possible futures: if your personal future consisted of many different worlds, then in what proportion of these alternative worlds would you get bowel cancer? This may be a bit shaky philosophically (and it is perhaps best to avoid ideas of parallel universes), but it personalises the risk while sticking to the simple concept of frequency.
Percentages versus frequencies
Probabilities can be expressed as fractions (eg 1/2), decimals (eg 0.5), percentages (eg 50%) or frequencies (eg 5 out of 10). It may seem these choices are irrelevant since they all express the same proportion, but it has been shown in experiments that the size of the numerator and denominator changes people's perception of the size of the risk. For example, people have been offered a prize for drawing a red ball from a bag, and then given the choice of two bags: one containing 1 red ball and 9 white balls, the other containing 8 red balls and 92 white balls. The majority chose the bag with 8 red balls, presumably reflecting a view that it gave more opportunities to win, even though the chance of picking a red ball was lower for this bag. Similarly, people confronted with the statement "Cancer kills 2,414 people out of 10,000," rated cancer as more risky than those told "Cancer kills 24.14 people out of 100". The potential influence of the size of the numerator and denominator is known as the ratio bias. Frequencies are generally used in risk communication, but it is important to keep a common denominator in all comparisons.
Framing the evidence
What would you prefer, a game in which you had a 10% chance of winning, or one with a 90% chance of losing? You may shake your head and say that they are exactly the same, but it has been shown that whether an outcome is expressed positively or negatively can make a big difference to people's perception. For example, in a classic experiment, one group of people were told:
"Of 100 people having surgery for lung cancer, 10 will die during treatment, 32 will have died after one year and 66 will have died after five years. Of 100 people having radiation therapy, none will die during treatment, 23 will die after one year and 78 will die after five years."
When framed in these negative terms, the risks of surgery appear large and 42% preferred radiation therapy. Others were told:
"Of 100 people having surgery, 90 will survive treatment, 68 will be alive after one year and 34 will be alive after five years. Of 100 people having radiation therapy, all will survive treatment, 77 will be alive after one year and 22 will be alive after five years."
When framed in these positive terms, surgery appears much more attractive and only 25% preferred radiation therapy.
Framing inevitably influences perception, so it is best to provide both a negative and positive description of the chance of an outcome.
A picture is a thousand words?
So far we have only looked at words, but each of the phrases we explored can also be represented by a picture. Pie charts are popular, and as we see below can reflect both a negative (getting cancer), and positive (being free of cancer) framing.
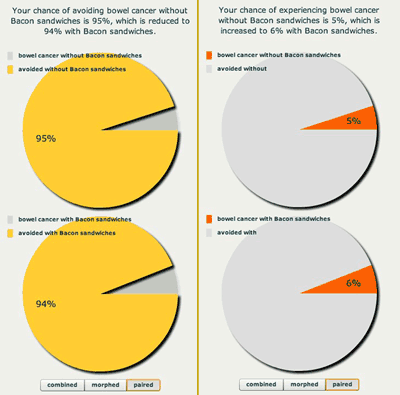
Positive and negative framing using a pie chart.
Column charts are again very popular, but as we see below, the perception of the importance of a change in risk can be manipulated by altering the scale of the column — the effect of eating bacon looks a lot larger in the second chart.
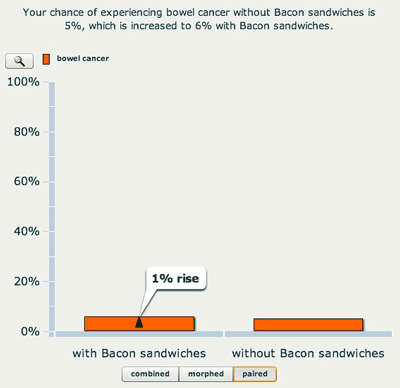
A column chart on a 0 to 100% scale.
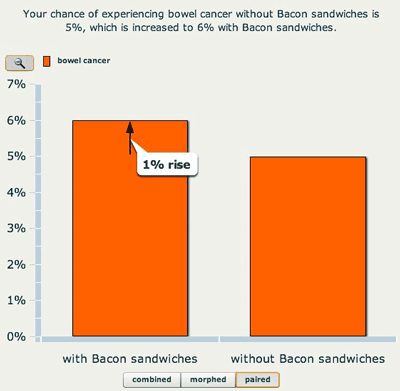
A column chart on a 0 to 7% scale.
Using frequencies naturally leads to using icons to represent people or possible futures. We have allowed blobs, tallies, smiley faces, and even photographs to further personalise the information. There is the choice to have the possible outcomes grouped or scattered: grouping makes them easier to count and can make the risks look larger. Colour can also influence perception.
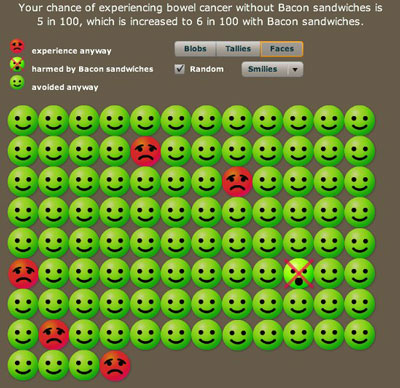
Your chances out of a hundred to contract bowel cancer. Smileys represent people who will not get bowel cancer, red faces represent those that will get it anyway, and the crossed out face represents people who will get the cancer because of bacon.
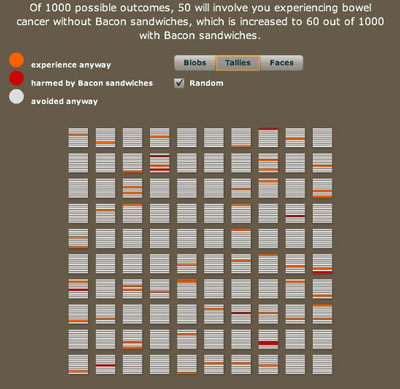
A thousand possible futures arranged randomly. Each future is represented by a horizontal line in one of the squares. Red means bowel cancer caused by bacon and orange means bowel cancer contracted regardless of bacon eating.
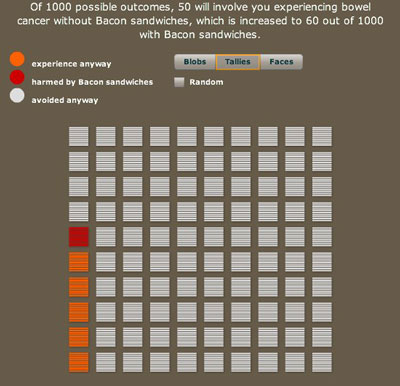
A thousand possible futures, this time tidied up so that all the red and orange lines are grouped together.
So what's the right spin?
Experts in the area of risk communication have reviewed all the research but have been able to draw few firm conclusions. People are different in their demands, tastes and understanding — there is no one-size-fits-all solution, and so it seems reasonable to use techniques that can be adapted to individuals. However, it is clear that certain practices should be avoided as they can clearly bias perception, for example mismatched use of relative and absolute risks, changing denominators, emphasising a negative or a positive frame, and so on.
It's also important to identify the aim of a particular bit of risk communication. Are we trying to interest people with attractive attention-drawing displays, or are we trying to increase their knowledge, or even change their behaviour? These multiple aims are not necessarily all achieved using the same technique.
And of course it is vital to remember that information plays a limited role in anyone's perception of the size and importance of a risk. Bigger influences will be their emotional response to the situation, their feelings of control, their dread of the outcome, how much they trust those giving the information, how familiar they are with the problem, what their friends and family think, and so on. But even if people are not going to take a very mathematical approach to the numbers, it still seems essential that they should have access to this information in a fair and balanced way.
Additional reading
There is a huge literature on risk presentation and we can only provide some pointers.
- An excellent resource is the polemical article by Gigerenzer and colleagues: Helping doctors and patients make sense of health statistics;
- A recent review article Numeric, verbal, and visual formats of conveying health risks: Suggested best practices and future recommendations by Isaac Lipkus is freely available;
- So is a more formal review from 2001, Presenting risk information. A review of the effects of framing and other manipulations on patient outcomes by Edwards and colleagues.
We are very grateful to Dr Tim Rakow for help with ideas and examples.
About this article
This article is adapted from material on the Understanding Uncertainty website.

David Spiegelhalter

Mike Pearson
David Spiegelhalter is Winton Professor of the Public Understanding of Risk at the University of Cambridge.
Mike Pearson created the animations for this article.
Mike, David and the rest of their team run the Understanding uncertainty website, which informs the public about all issues involving risk and uncertainty.
Comments
Anonymous
Out of 100 patients, 101 have some result? (Framing The Evidence section)
Marianne
The 78 that will have died after five years include the 23 that will have died after one year, so the two don't need to add up to 100.