When you first learn about it, maths can appear to be a solid edifice of knowledge – complete and unchanging. But sometimes even basic questions remain unanswered and it is always very exciting when such an answer might be just around the corner. We were lucky enough to speak with Oscar Randal-Williams, our neighbour here in the Centre for Mathematical Sciences at the University of Cambridge, who is tantalisingly close to such an answer.

Randal-Williams works in topology – the area of maths which studies what properties remain unchanged when you are allowed to bend, stretch or squash an object, but you do not cut or tear it. Famously a donut (one with a hole in the middle) is topologically the same as a coffee cup – if they are both made of malleable clay you could bend and stretch one into the other. But they are topologically different to a ball – you can’t turn a ball into a donut without tearing or cutting a hole.

Topology in action

All of these – donuts, coffee cups and balls (or more accurately the surfaces of these) – are examples of topological spaces. But the most basic spaces in topology are the same ones you learned about in school – Euclidean spaces. These are the most concrete of spaces, pinned down by some number of coordinate axes like the vertical and horizontal axes you used at school when drawing graphs. The dimension of your space is given by the number of coordinate axes you need to map it. Randal-Williams is trying to answer the question: what are the symmetries of Euclidean spaces, particularly of higher dimensional spaces of five or more dimensions?

Smooth symmetries

Rotations, along with reflections, are the symmetries that we instinctively think of but what does that mean when applied to a Euclidean space? Consider the three-dimensional Euclidean space that we are all familiar with, with two perpendicular horizontal axes (for forward-back and left-right) and a vertical axis. Then every point in that Euclidean space is written in terms of these three axes. Rotating these three axes by, say 45 degrees, around some axis of rotation leaves the space essentially unchanged.  For example everything is still the same distance apart and the coordinate axes are still straight lines that are all perpendicular to each other..  The rotation acts as a symmetry of the Euclidean space.

Rotation and reflections, and their generalisation, to higher dimensions, are called smooth symmetries. We can think about how all these smooth symmetries relate to each other by imagining them as points in a space. You can imagine starting at the rotation described above and moving slightly in this space of symmetries. This might take you to a rotation of slightly more or less than 45 degrees, or one where the axis of rotation is moved a little bit. "Then that's a similar rotation – it’s not the same but it's nearby to the one you had before," says Randal-Williams. "It makes sense to think about walking about in the space of symmetries." This space of smooth symmetries of Euclidean spaces has been well understood for roughly a century – mathematicians have a description of the space in terms of its topology.

Continuous symmetries

But there's another type of symmetry, called continuous, that is much more difficult to understand than smooth symmetries: "You can't really think about continuous symmetries directly, it's like looking at the sun somehow!" Continuous symmetries are hard to imagine. Like smooth symmetries, continuous symmetries have to send nearby points to nearby points. But they can behave far more strangely, in the sense that they could, for example, send an axis to some very jagged curve.

You can't look directly at the sun! And you can't really think about continuous symmetries directly! (Photo of annular eclipse in 2019 by Rehman Abubakr – CC BY-SA 4.0

The space of continuous symmetries includes all the smooth symmetries, but mathematicians have known since the 1970s that there are continuous symmetries that aren’t smooth. But we don't have, as of yet, a description of the space of continuous symmetries of Euclidean space. 

For mathematicians, including Randal-Williams, describing all the symmetries of Euclidean space, not just the smooth symmetries, is a basic question to ask. "My main motivation is being outraged by not knowing things!" he says. "And this is such an utterly basic thing, a really fundamental understanding of what we mean by symmetries of these spaces." 

Euclidean spaces can be thought of as the most basic case in topology, which deals more generally with manifolds ( that is, anything that looks locally like a Euclidean space). "So if you can answer the question for Euclidean space you're on the way to answer much more."  

Randal-Williams and his colleagues are now tantalisingly close to a complete description of the continuous symmetries for every Euclidean space of any dimension of 5 or more. "We haven't quite proved it in complete detail but it makes so much internal sense I'm confident it must be right."

Rephrasing the question

As it's so hard to consider continuous symmetries directly, Randal-Williams and his colleagues Alexander Kupers and Manuel Krannich instead found a way to rephrase this question. It turns out that understanding the continuous symmetries of Euclidean space is more or less interchangeable with understanding smooth symmetries of a disc (the mathematical name for the region inside a circle in two-dimensions, and the generalisations of this to higher dimensions). 

Using this new point of view, Randal-Williams and his colleagues were able to develop and find strong evidence for their conjecture: that the space of continuous symmetries of any high-dimensional Euclidean space can be expressed in terms of algebraic objects called graph complexes. 

Graph complexes have only really been studied in any detail in the last 10 to 15 years. (We are now talking about a different mathematical graph here – this graph is what you might normally call a network.) "They are built out of graphs – in the sense of blobs and sticks between them" says Randal-Williams. Graph complexes are built from finite graphs –  graphs with finitely many blobs (nodes) and sticks (edges) between them – and an operation that captures all the ways of contracting an edge. 

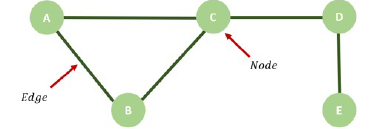
A network (or graph) with five nodes and five edges.

The incredible thing about these graph complexes is that they are so elementary, says Randal-Williams. The definition above is very vague, but even a rigorous mathematical definition is surprisingly easy to state for mathematicians. "And the same graph complexes show up in surprisingly different bits of maths. And I don't just mean the same kind of thing, I mean literally the same graph complex." 

Surprising connections

The graph complexes from his work on symmetries of Euclidean spaces also arise in mathematical physics (which is where graph complexes first emerged), and are related to questions in other areas of mathematics, such as algebraic geometry (the area of maths that uses algebra to study geometry). "It's incredible it's literally the same [graph complex] that answers these different questions. In particular it shows that those questions are in some way related, because they are both related to the same little combinatorial object." But if you were not to consider graph complexes, it would be very difficult to see how these areas of mathematics related to each other. "It really is some sort of primitive thing. It's like the prime numbers – it's a building block that shows up in lots of different buildings."

The fact that graph complexes provide the description Randal-Williams and his colleagues were looking for is quite surprising. "The connection is quite indirect. Why should the symmetries of Euclidean spaces have anything to do with finite graphs? That is not obvious at all." They are now working on the next steps to prove their conjecture by working with the world expert on graph complexes, Thomas Willwacher. Stay tuned – we will keep you posted on when they prove that they have answered this fundamental question in topology!

Oscar Randal-Williams

About this article

Oscar Randal-Williams is the Sadleirian Professor of Pure Mathematics at the University of Cambridge. You can find some of the mathematical details about the work that was explored in this article in his paper from the 2022 International Congress of Mathematicians, in his paper with Manuel Krannich from 2021, and in his paper with Alexander Kupers from January 2024.

Rachel Thomas is Editor of Plus.