Could these be arranged more efficiently?

When you are packing oranges into a box, you're faced with a problem. Because the oranges are round, there'll always be gaps between them, so you can't possibly fill up all the available space. What's the best you can do? The answer is at most 74%: even the cleverest packing arrangement won't be able to fill more than around 74% of the space in the box. In precise mathematical terms, when packing equally-sized balls into space, the highest proportion you can hope to fill is $\pi/(3\sqrt{2}) \approx 0.74.$

This seemingly humble result exercised mathematicians for centuries. It was first suggested by Johannes Kepler in 1611, but it wasn't until 1998 that the mathematician Thomas Hales found a formal (though controversial) proof that it is really correct.

Now it appears that a mathematician at the Humboldt University of Berlin has cracked an extension of the problem. Maryna Viazovska says she has proved that if you're trying to pack eight-dimensional balls into space, the best packing density you can achieve is $\pi^4/385,$ which corresponds to approximately 25%.

But what is an eight-dimensional ball? It's a good question, because this strange object is not something we can visualise. In ordinary three-dimensional space every point is given by three coordinates. Although you can't visualise higher dimensional spaces, there's nothing to stop you from defining them in a similar way. Points in eight-dimensional space are defined by strings of eight numbers. Using the distance measure in three-dimensional space as an analogy, you can define what you mean by the distance between two points in eight-dimensional space (see the box). Similarly, you can define a way of working out the volume of a region of eight-dimensional space.

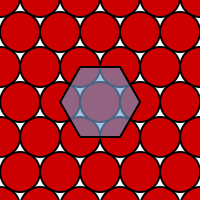
This arrangement of discs gives the highest packing density in 2D space. The centres of the circles form a hexagonal lattice.

A ball in three-dimensional space has a centre point and a radius. The ball consists of all the points whose distance from the centre point is less than or equal to the radius. In the same way you can then define a ball in eight-dimensional space: it has a centre point and a radius and consists of all the points whose distance from the centre point is less than or equal to the radius. You can then ask yourself the ball-packing question: if you are packing eight-dimensional balls into eight-dimensional space (the balls are not allowed to overlap) what's the highest proportion of the space you can fill? (When mathematicians answer this question, they don't try and see how many balls they can fit into a box, but instead see what proportion of all of the infinite space that is available can be filled.)

Viazovska's result is the first to put an exact number on the packing density for a space of dimension larger than three. The 25% may seem a bit low, but there is a downward trend. One-dimensional space is simply a line, and a ball in this space is an interval. Since you can fit intervals together side by side to cover the whole line without leaving any gaps, the packing density in this case is 100%, corresponding to a proportion of 1. In two-dimensional space, that is, in the plane, the balls are discs. The most efficient way of arranging them is shown on the right, and it gives you a packing density of around 90%, corresponding to a proportion of $\pi/(2\sqrt{3}).$

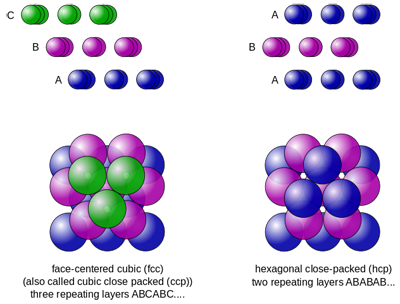
Two optimal packings of balls in 3D space. Image: Cdang, CC BY-SA 3.0.

In three dimensions there are many different optimal packings. Two of them, the cubic close packing and hexagonal close packing, are shown on the left, and as already mentioned, give a packing density of around 74%, corresponding to a proportion of $\pi/(3\sqrt{2}) \approx 0.74.$ The reason why Thomas Hales' 1998 proof of this fact was controversial is that it was largely done on a computer. It consisted of 250 pages of traditional pen-and-paper work and over 3 gigabytes of computer code and data. Since no human can possibly check the computer's calculations in their life time, mathematicians were unsure about whether the result could really be considered as proven. Even today, the role of computers in mathematical proof continues to be a hotly-debated topic (see Welcome to the maths lab and The future of proof).

Viazovska's paper, at a mere 21 pages, seems tame in comparison. It has been posted online and is awaiting scrutiny from other mathematicians.

And just in case you wondered: yes, there are practical reasons for thinking about ball packings in higher dimensions. They are useful in communications technology. See here to find out more.

We've just heard that Viazovska's method has been used to also solve the problem in dimension 24. We'd like to thank out friend Andreas Loos for pointing this out to us, and also for pointing us to the original result. You can see Loos' article (in English) on the website of the Deutsche Mathematische Vereiningung.