
The physics of language
If you want to understand languages, to capture the signature that makes a language unique, who should you talk to? Should you talk to someone who speaks it as their first language? Or someone who had to learn it recently? Should you talk to a linguist who understands the way languages are structured? Or should you talk to a computer scientist using machine learning to automatically extract meaning from the vast banks of text that are now available online?

Sanjaye Ramgoolam
One person you might not think of talking to is a theoretical physicist. But Sanjaye Ramgoolam, from Queen Mary, University of London, is bringing unique insights from his work as a physicist to developing an exciting new approach to understanding language.
Ramgoolam has spent much of his career working in string theory, a theory that attempts to unite our understanding of the very large (cosmology) with our understanding of the very small (quantum physics), under one mathematical umbrella. (You can read about his work in theoretical physics here.)
Recently Ramgoolam has collaborated with computer scientists, Dimitri Kartsaklis and Mehrnoosh Sadrzadeh, to develop linguistic matrix theory – applying ideas from the mathematics and symmetry found in quantum physics to understanding the language data built by computer scientists using AI techniques.
Writing words as numbers
Ramgoolam was intrigued by the huge datasets generated in natural language processing (NLP), where machine learning techniques process the vast amount of natural text (that is, written by people) that is available digitally. One of the primary goals in NLP is to automatically extract the meaning of the text.
"You shall know a word by the company it keeps," was an insight of the influential British linguist, John Rupert Firth. We would expect the words "dog" and "cat", both describing types of pets, to be used in similar ways, occurring close to the same set of words when written in text.
I want a pet dog/cat.
Don't forget to feed the dog/cat before you go out.
This idea is now used in NLP. We can capture the meaning of a word by constructing a vector (a list of numbers) describing that word's proximity to other words: the vector is a mathematical representation of the company it keeps.
The first step in this process is to identify what are called context words. You might use only a few hundred of context words, or you might use thousands. The number of context words you use gives you the size of the vectors you will produce for each word in the language. Then your algorithm looks up each word, and counts how frequently it occurs in the vicinity of the first context word, in the vicinity of the second context word, and so on, building a sequence of numbers.

A "dog" and a "baby" – they mean different things.
Consider a very simple example: suppose you have just two context words: "pet" and "feed". Then the words "dog" and "cat" would occur frequently with these context words and the vectors you'd get for "dog" and "cat" would be similar.
Now another word with a different meaning, such as "baby", would occur frequently with "feed", but it would rarely occur with "pet". "The sequences of numbers capture something about meaning," says Ramgoolam. "And this is the idea that underlies distributional semantics."
To illustrate this idea, here is an example of what the vectors for the words "dog", "cat" and "baby" might look like based on a collection of texts:

Meaning from matrices
But, as anyone learning a language knows, having an excellent vocabulary doesn't mean you can speak a language. The meaning of language is also about how you combine those words.
In 2010 Mehrnoosh Sadrzadeh and her collaborators in Oxford thought about how to capture this composition of words with data. Some words, such as adjectives and adverbs, are only used in combination with other words. What Sadrzadeh and her colleagues at Oxford realised is that grammatical composition of words has a lot of similarity with the composition of vectors and matrices (an array of numbers) and tensors (higher-dimensional matrices) in mathematics.
Let's return to the vectors that we’ve already built using the proximity of words with context words, such as our examples of vectors for "dog" and "cat" above. These are nouns, but you can also have a phrase that behaves like a noun, such as "black dog" and "black cat". You can use the same process to build a vector for these noun phrases, based on how often these phrases appear near the context words.
"You do this for 'dog' and 'black dog', and 'cat' and 'black cat', and other pairs like that," says Ramgoolam. And then you try to find a matrix representing the adjective "black", such that that matrix composed with the vector for "dog" produces the vector for "black dog". And so that the same matrix composed with the vector for "cat" produces the vector for "black cat". More generally, we want that our matrix composed with the vector for some word X, produces the vector for "black X".
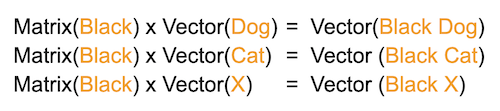
"In this way you can build a matrix that represents 'black'," says Ramgoolam. Using this approach you can represent a language as a set of vectors, matrices and tensors (which, respectively, you can think of as one-dimensional, two-dimensional, and higher-dimensional matrices) that represent the meaning of the words and the way they combine together.
This technique can be applied to the vast digital collections of texts, such as Wikipedia which has over alone has six million articles in English, to generate huge datasets representing language as matrices and vectors. These datasets were first created by computer scientists and linguists to automatically extract the meaning of words in a language. But when Ramgoolam examined this NLP data he recognised something familiar, something from his background as a physicist. Find out more in the next article...
Sanjaye Ramgoolam explains how he is using techniques from physics to give new insight into language
About this article

Dr Sanjaye Ramgoolam is a theoretical physicist at Queen Mary University of London. He works on string theory and quantum field theory in diverse dimensions, with a focus on the combinatorics of quantum fields and the representation theory of groups and algebras. One of his recent research directions, sharing some of these mathematical mechanisms, is the development of an approach to the study of randomness and meaning in language.
Rachel Thomas is Editor of Plus.