
Police and thieves continued
What lessons can we draw from the mathematical model described on the previous page? Simulating reality using the grid model requires lots and lots of calculations, but there is a way of turning it into a system of two equations that are easier to analyse. The idea is to shrink the time steps, as well as the space between points, to zero and derive a continuous version of the model. The grid turns into a piece of the plane, and each point on that plane comes with an attractiveness value. You also get a burglar density which measures the number of burglars there are at a given point at a given time.
The new model consists of two interlinked equations (partial differential equations to be precise) which describe how the attractiveness value of a location and the density of burglars at a location change over time (depending on a number of parameters).

Reaction-diffusion processes have been used to describe the formation of patterns on animal coats.
Interestingly, the equations you get have the same form as those describing reaction-diffusion processes you see in chemistry or biology: here two substances spread out (diffuse) through space and react with each other when they meet. Reaction-diffusion processes are well-known for creating patterns. The spots and stripes on animal coats have been described as such a process, involving two substances that stimulate or inhibit the production of pigments in the animal skin (see here). That's good: after all, it's the patterns of crime hotspots we're trying to understand.
The way to think about reaction-diffusion in a crime context is this. Both the risk of crime (given by the attractiveness value of a location) and the density of burglars diffuse through space — they are like the two chemical substances. And when risk meets burglar the two can interact, causing a crime. Using this idea, Bertozzi and her colleagues built a more sophisticated model in which targets can also move around. This means they can represent, not just houses, but also cars or people. So a wider range of crimes, not just burglaries, can be represented. (You can find out the details in this paper.)
When you use this model to understand crime, you see why hotspots form. Each individual crime comes with a "region of influence", shown in the figure as dashed circles whose average area depends on the parameters and the relationships between them. If the parameters conspire to produce regions of influence small enough so that they don't overlap, then no hotspots form. That's because clusters of risk just don't emerge. If the regions of influence are large enough to overlap a lot, so risk spreads out more or less uniformly, then hotspots won't form either. It's only when those regions overlap a little, so that they link individual crimes locally but not over larger distances, that hotspots from local crimes.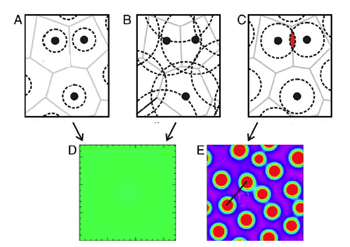
When the regions of influence don't overlap or overlap a lot (A and B) then there are no hotspots (D). If they overlap just a bit then hotspots do form from local crimes (E). (Image from Dissipation and displacement of hotspots in reaction-diffusion models of crime, by Bertozzi et al published in The Proceedings of the National Academy of Sciences Online.)
Another thing the model suggests is that there are two types of hotspot. One type forms when the system is quite unstable — susceptible to small variations — and they can emerge when a local area experiences just a small spike in crime. The other type forms when the system as a whole is stable, but there's a large spike of crime in a particular neighbourhood.
The distinction is important. The model also suggests what might happen when police move in to suppress a particular hotspot. If the system is generally stable, the hotspot would indeed disappear as a result of police action. If the system is unstable, however, the hotspot first turns into a ring around its original centre, and then breaks up into smaller hotspots: police action, in this case, has only displaced crime to other areas. This makes sense, as in the unstable case, a small spike in crime in a part of the "hot ring" can produce a new hotspot. So perhaps police should investigate what kind of hotspot they are dealing with before taking action.
The insight into the different types of hotspot is something you get from looking at the underlying equations and the dynamical system they define. It's not something you'd see just by looking at crime statistics. So even a basic mathematical model, based on simple assumptions, can give you ideas you otherwise might not come across.
Further reading
The following two academic papers are reasonably accessible for someone with a bit of a maths background.
- A statistical model of criminal behaviour by Bertozzi and colleagues describes the discrete model explored in the first part of this article.
- Dissipation and displacement of hotspots in reaction-diffusion models of crime, also by Bertozzi and colleagues, describes the continuous model.
About this article
This article was inspired by Andrea Bertozzi's Rouse Ball Lecture, which took place in Cambridge in April 2015.
Marianne Freiberger is Editor of Plus.