
Proof by picture!
Drawing pictures is incredibly useful when doing maths. They help build your intuition, allow you to have fun playing around, and sometimes pictures can even serve as proof. Below is a selection of articles exploring proofs in which pictures play an important role.
If you'd like to try your own hand at some picture proofs, then head over to our sister site NRICH, which has a great collection of problems for ages 11 upwards.
Seeing Pythagoras — Here are three geometric proofs of Pythagoras' theorem. No algebra necessary!
Seeing proof — Having trouble with algebra? Then try these visual proofs of two well-known algebraic identities.
Some lovely proofs by picture — Don't like trigonometry? Don't worry, here are three beautiful proofs of a well-known geometric result that make do without it.
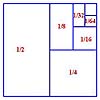
Outer space: The rule of two — The idea that an infinite sum can converge can be a little hard to grasp. Luckily, when it comes to a well-known geometric series, there's a neat visual demonstration.
What is the area of a circle? — You might know the formula for the area of a circle, but why does this formula work? Our visual explanation really is a piece of cake, served up with a hefty estimate of pi.
The art gallery problem — A beautiful result where a clever shift in viewpoint coupled with some geometric intuition delivers the proof (almost) on a plate.
Trisecting the angle with origami — You can't divide an angle into three equal parts using traditional geometric methods. But you can do it with origami! The best way to do this is to try it and see. Here's how.
Maths in a minute: Euclid's axioms — Finally, no talk of geometric proofs would be complete without a nod to Euclid's axioms of geometry and a couple of examples of what they allow you to do.