David Sloan has a great response for someone asking him what he does for a living: "I calculate how likely it is that the Universe exists." This impressive job description comes from Sloan’s role as a post-doctoral researcher at the University of Cambridge working on the project, Establishing the Philosophy of Cosmology. The project aims to bring together philosophers and cosmologists to engage with the big philosophical questions in the area. Sloan is working on the measure problem in cosmology: "How likely it is, given a random set of initial conditions, that you would end up with a universe that looks rather like ours."

This simple idea immediately conjures a whole range of questions, philosophical and cosmological: How do we predict what universe we will end up with, starting from some initial conditions? How do we calculate the probability of such a universe looking like ours? And just what do we mean by a "universe like ours" anyway?

How did we get here?

The evolution of the Universe is described by the Friedmann equations developed in 1922 by Alexander Friedmann. He used Einstein's theory of general relativity to predict that the Universe was expanding. At the time this was a revolutionary idea, leading Einstein to dismiss Friedmann's equations as a "mathematical curiosity" but today this is part of our standard picture of cosmology. (You can read more about this in What happened before the Big Bang?.)

The equations describe how the Universe evolved during the early phase of inflation, the brief period of massive expansion that occurred shortly after the Big Bang. Echoes of the resulting structure were encoded in an initial burst of radiation which is known as the cosmic microwave background radiation (CMB). "My work was to look at what range of initial parameters led to observations, such as those of the CMB as seen by the WMAP and Planck satellites, and how we can put a probability measure on this." (You can read more about this in What Planck saw.)

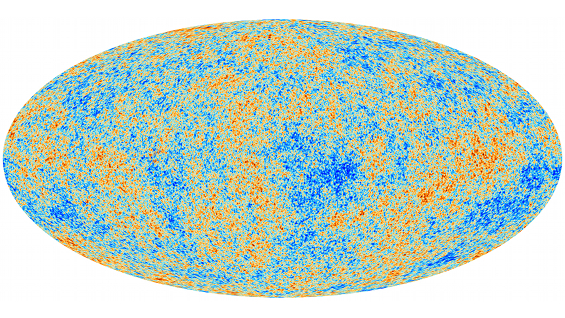
The all sky map of the temperature fluctuations in the CMB, as seen by Planck. (Image credit ESA and the Planck Collaboration)

There are many possible solutions to the Friedmann equations, each representing a possible universe. Some may be like ours, others may be quite different, say only lasting a few moments, or one where galaxies and stars never form. Together all these form a space of possible solutions. Universes with different properties form different regions in this space and the relative volumes of these regions represent the relative probability of that type of universe will evolve, according to our model. Sloan works out what these solution spaces look like, identifying these different regions, and how to calculate their volumes to give the probability that universes with particular sets of properties will evolve.

The actual calculations he works with are very complicated. But you can picture it, vastly simplified, in terms of the possible values some parameter could take. Suppose a parameter, let's call it $x$, goes into our model of universe evolution, and that $x$ can be any value between 0 and 1. Then the properties of the resulting universe might depend on the value of $x$, say, if $x\leq 1.4\times 10^{-11}$ then there is not enough inflation to match the observations we see from satellites in our Universe. While if $x \ge 1.4 \times 10^{-11}$ then enough inflation occurs, resulting in a universe producing observation like those we've seen like ours. So when considering the range of values that our parameter $x$ can take, it is overwhelmingly likely (with a probability of something like 0.99999) that this model gives a universe like ours. (You can read more of the details in this article in New Scientist and the paper it's based on. And you can find our more about how our Universe evolved in the Plus article, From planets to universes.)

You are here

But what exactly do we mean by a "universe like ours"? The pragmatic way to answer this is to say it is a universe that results in observations like those we have observed in our own. Data like the cosmic microwave background radiation (the CMB) has dramatically shaped the picture we have of our own Universe. And any universe "like ours" should also generate the same observations we see in the CMB and other data sources. One complication though, is that we only have our Universe to look at, we don’t have any alternative examples to compare to, or probe for information.

"One of the things that cosmology has that's different from the rest of physics, and actually puts us much more in line with, say, the social sciences, is that we can only really do natural experiments," says Sloan. "We can't design a universe. We can't build a machine, put some initial conditions in, fire it up in a lab and see what happens. We can only observe the Universe as it is."

This is a similar situation to astronomy, but with one significant difference: "Astronomers don’t get to build stars and see what happens, they can only observe them. But they have lots and lots of stars to look at. In some sense, we have precisely one data point: the one universe we live in. And as anyone who has done GCSE science will tell you, one data point is pretty terrible for doing science."

Image from NOAA

This lack of other data points requires a different approach and it is here that a philosophical perspective can be so useful. The problem of having such a convincing piece of evidence – that our Universe exists – and a lack of any other evidence, could lead to the interpretation that the Universe is fine-tuned for life. If you consider the abundance of carbon in the Universe you might think that abundance is a miracle as carbon is necessary for life, as we know it, to exist. "If we tweaked the parameters this way or that way there wouldn’t have been any carbon and we wouldn’t be here," says Sloan. But this interpretation can start to look shaky with a change of perspective. "There's a good point made by [Douglas Adams] which is that suppose there's a puddle sitting in a hole. It would ask, 'Wow! Isn't it amazing that there's a hole just this shape that I fit into it? This hole must have been designed for me.' " So rather than explaining our perfectly tuned Universe by invoking some benevolent creator, you can instead call on something called the anthropic principle: that our Universe has to be favourable to life, as otherwise we wouldn't be observing it.

Instead it is necessary to take a step back, and consider how broad a spectrum of possible universes resulting as solutions of the Friedmann equations would be acceptable. Are we only interested in universes that we would could exist in, or would any universe that allows for some intelligent observer be one of those we should allow for, humanity just being one particular example of such an observer? "If I do a calculation and [find that if] this number were three instead of seven then everything would be the same but we would be green, would we say that's acceptable or not? Or if different numbers had come out but in those cases the living things would have been built out of silicon instead of carbon. Of course, these kinds of questions are phenomenally difficult to actually get a handle on, we don't have the technology to evolve things to the point of life and so on. But what you can say is, under [certain] conditions there would be far too much radiation, and so we could rule out, at least, life as we know it. And under [other] conditions stars would only last for 15 seconds, so we can rule out anything having evolved under those.”

Why are we here?

This all sounds like a good game for philosophers and for those seeking to explain our place in the Universe, but Sloan's research also provide us with a practical tool for testing our theories of physics. "[Exploring the measure problem] actually gives you a degree of confidence, or lack of confidence, in the explanatory power of your models of physics," says Sloan. For example, suppose his calculations said that, given a particular model of physics, it is incredibly unlikely that a universe like ours evolved (ie, that the probability of such a universe evolving was very close to zero). Then we can ask ourselves, is it more likely that the model is right and we ended up here despite this tiny probability, or is it more likely that our model was wrong in the first place?

"If I said, either physics is wrong or I rolled a die six billion times and it came up six every time, then which of these is more likely? It's more likely that physics is wrong and at that point, as a scientist, you would throw away the physics." So these probability calculations open a window on questions that we otherwise might not be able to interrogate, providing a way to test the untestable.

The current map of the Universe. Image courtesy NASA.

"The nature of these things is normally that the probabilities turn out to either be very close to zero or very close to one," says Sloan. If the probability turns out to be close to one they you can rest easy that your model of physics provides a good explanation of the evolution of the Universe. For example Sloan has used this approach to examine theories of loop quantum gravity, where the Universe bounces from contracting to expanding instead of starting from an initial big bang. The advantage of this theory over others is that you can do calculations at the point of the bounce, where other theories break down. "There you find there is an incredibly high probability of the Universe looking the way it does currently. [Given the assumptions of the model] then the probability you get the WMAP observations is about one minus something like one part in a million. So it's a really, really, really, highly likely thing," says Sloan. This is a great relief to proponents of this theory: "It says that, yes, if this is the right theory of physics, don't worry. Observations haven't told you to throw away [this theory of] physics."

Eventually, Sloan would like to develop a kind of black box to tackle the measure problem. "One thing that would be very nice, but will take a lot of work, is to create a method of taking in fundamental models of physics – your string theories, your causal set theories, your no-boundary proposal... all of these extensions to general relativity – taking these in, turning the handle, and it spits out a number for you. It tells you 'This is incredibly probable' or 'This is not incredibly probable.' Because then you could use [this box] as a test of some of the theories that [otherwise] are very much un-testable."

Investigating the measurement problem allows us a glimpse of the answer to the biggest question of all: why are we here? Who knows when we will answer that question, but Sloan's research will definitely give us a hint.

About this article

David Sloan was interviewed by Rachel Thomas, co-editor of Plus, in September 2013.

David Sloan is a member of the Department of Applied Mathematics and Theoretical Physics, working on the Establishing the Philosophy of Cosmology project.