Last week I got an AI to write an autobiography of my cat. The result was impressive: brilliantly written with some passages uncannily, even spookily, accurate. That's even though I'd only given the AI a paragraph's worth of information to go on.

But there were also the kind of glitches you'll be familiar with if you've played around with AI. One passage, exploring my cat's love for the underfloor heating in the bathroom, reads, "The tiles are cool against my paws, a welcome contrast to the warm floor." But that's nonsense. The whole point of underfloor heating is to warm up the floor tiles, and that's why my cat loves it.

AI without physics

The problem here was that the AI has no experience of the physical world. It learns to perform its task purely from data, in this case a huge volume of quality text written by humans. It reproduces the patterns it finds within language with amazing success. Sentences make sense and form a (mostly) coherent story. But the AI has no idea what its outputs mean. In particular, it has no knowledge of physics, and no way of checking whether its output makes physical sense.

When it comes to amateur writing such a lack of knowledge isn't earth-shattering. But there are also potential applications of AI that are all about the physical world. Examples are weather forecasting or applications in engineering, such as checking if an aircraft design is structurally stable. For these applications it seems desirable, even essential, to provide AI with some of the vast knowledge of physics we humans have accumulated over millennia.

This is why mathematicians are currently busy building physics-informed neural networks. A neural network is a type of algorithm, originally inspired by the neurons in our brains. Neural networks are used in machine learning, the approach to artificial intelligence that has seen so many successes in recent years. The large language models that power ChatGPT and the book writing app, as well as models used in areas such as weather forecasting, are all based on machine learning. Physics-informed neural networks are known as PINNs for short.

AI versus physics

Weather forecasting is a good example to illustrate PINNs. Traditional weather forecasts are based on our understanding of the physical processes that determine the weather. These are described in the language of mathematics, using differential equations (see our short article on numerical weather prediction). But because the weather is an extremely complex (actually chaotic) system, and because the equations are incredibly difficult to solve, forecasts lack accuracy and require enormous computing power. This is why the Met Office has a very expensive supercomputer.

On the other hand we do have vast amounts of data about the weather. Machine learning algorithms could crunch through this data, learning important patterns during their training phase, such as how the amount of cloud in a region depends on parameters like temperature and pressure. Once the training is complete, they could then use this information about patterns to produce forecasts in the real world.

That's the theory, but although there have been significant advances in using AI in weather forecasting, we're still some way away from replacing traditional methods (see Predicting the weather with artificial intelligence to find out more.)

AI with physics

The idea behind PINNs is to equip the algorithms with knowledge from physics while they are doing their learning. "If we have a differential equation that describes the [physical] system, we can incorporate that into the training phase of the neural network," says Georg Maierhofer of the universities of Oxford and Cambridge, who is also a member of the Maths4DL research project, which works on the mathematics behind machine learning.

There are various advantages to be had from this approach. Traditional weather forecasting is limited by the knowledge we currently have about atmospheric processes — this is what the mathematical weather models are built on. These models are also always a simplification of reality. The weather depends on a multitude of factors whose interaction we don't always understand. Taking account of all of them in a mathematical model is an impossible task.

The advantage of a PINN is that it wouldn't have to rely on known physics alone, but could also mine the information hiding within existing weather data. It might therefore spot connections we don't know about, or which we don't know how to incorporate in the mathematical models. "The possible advantage of neural networks in this setting is that they might come up with some better, unusual approaches for these kinds of problems that might be more efficient, might be less computationally expensive, might be quicker, or more reliable in the long run," says Maierhofer. "This flexibility is one thing that is really nice."

In addition to finding new approaches, PINNs can also help with the physics that we do know. The differential equations that govern the behaviour of the Earth's atmosphere (the Navier-Stokes equations) are incredibly hard to solve. There's no chance of finding solutions with pen and paper or a few lines of computer code. Instead, a method called computational fluid dynamics is used in practice to provide approximate solutions, but this can require immense computing power.

The power of machine learning can be brought to bear here too, with PINNs providing alternatives to computational fluid dynamics for finding solutions to these tricky equations. More generally, building neural networks that can learn to solve differential equations is a major focus of the Maths4DL research project.

Hallucinations…

As it stands, PINNs are still in their infancy. They were first proposed in 2017 and research has only really taken off in the last five years or so. "There are significant opportunities, but [PINNs are not yet] able to compete in a large-scale industrial setting with anything that's been there classically," says Maierhofer. "We see some early advantages in using PINNs in a research-based setting but they are unable to scale up and provide the same reliability and certifiability that you have with classical methods."

One major challenge is that there aren't enough theoretical guarantees that a PINN won't give you false information. The large language models that drive ChatGPT (or the book writing AI mentioned at the start of this article) can suffer from so-called hallucinations: they make up information that seems real, but is actually false. When a friend of mine got an AI to write a book about himself, the algorithm produced a hallucination in the shape of a daughter my friend doesn't have.

"The same phenomenon can occur when you use machine learning methods to simulate physical systems," says Maierhofer. "For example when you want to simulate the flow of a fluid, then the machine learning method might give you something that to the eye looks correct, but might have the wrong pressure in certain areas. [In meteorology] this might mean it's missing a significant weather system over part of the UK, for example." In other applications, such as the design of aircraft, such a mistake could prove disastrous.

…and holes

Another challenge facing PINNs is that they can, quite literally, get stuck in a hole. During the training phase machine learning algorithms learn how to make their outputs more accurate. They do this by minimising a loss function, which measures the inaccuracy of their outputs. As a metaphor, imagine the algorithm feeling its way through a hilly landscape: at the peaks of the landscape the inaccuracy is high and in the valleys it's low. The aim is to reach the deepest valley of the landscape. The trouble is that the algorithm can only feel which way is up or down in its immediate vicinity. When it has reached the bottom of a small dip, it may then think it's reached the lowest point in the entire landscape, when really there's an even deeper valley further afield — you can read more about this problem in Maths in a minute: Stochastic gradient descent.

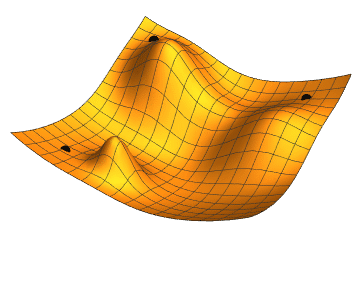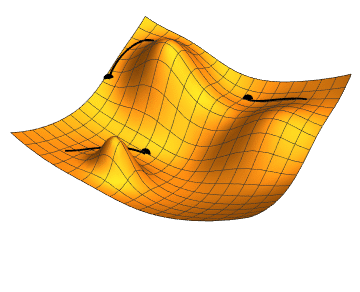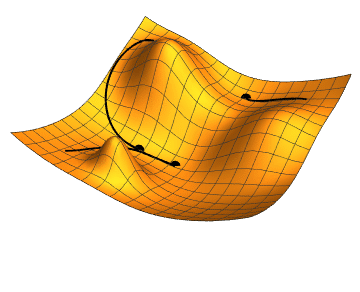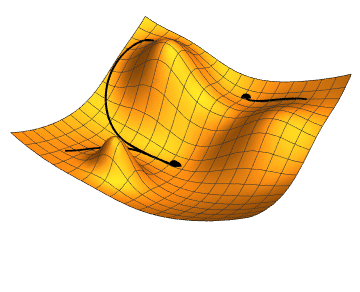
An illustration of gradient descent, the method which helps machine learning models to improve their outputs. The dot in the top right gets stuck in a small dip, rather than finding the deepest valley. Image: Jacopo Bertolotti

Once an algorithm has got stuck in this way, no amount of computing power will help it out. That's in stark contrast to classical methods. "In classical methods there's this paradigm that if you increase the computational resources, by letting the algorithm run [longer] or giving it a few more computers to run on, you typically get a more accurate answer," says Maierhofer. "In machine learning methods there's a barrier that currently people cannot break. It seems that after you've reached a [certain] point of giving the computer more resources, these extra resources [no longer help]. With current methodologies this is a big problem."

Combining forces

Despite these challenges, or perhaps because of them, PINNs are currently generating a lot of excitement in the research world. "It's a really interesting time to work on PINNs because they are so young," says Maierhofer.

This excitement, as well as the promise, of PINNs attracts researchers from a variety of fields. We met Maierhofer at a workshop he organised, as part of the Maths4DL research programme, that involved people from industry as well as academics. "My goal was to try and bring in people from as many backgrounds as possible. There are really tough challenges with machine learning methods and the more different points of view and experiences we bring in, the more likely it is we find a good resolution to these challenges." Once PINNs become good enough to implement, they could help with applications beyond weather forecasting or engineering, for example in biology and chemistry.

Perhaps they will even be brought to bear on the models that can write books. In that case my cat will one day be able to enjoy an autobiography that is physically correct. Imaginary daughters, unless they break the laws of physics, will have to be dealt with by different means.

About this article

Georg Maierhofer is Hooke Research Fellow working in the Numerical Analysis Group at the University of Oxford and a Henslow Research Fellow on leave from Clare Hall within the University of Cambridge.

Rachel Thomas, Editor of plus.maths.org, interviewed Maierhofer in spring 2024. 

Marianne Freiberger, also Editor of plus.maths.org, wrote the article based on this interview and Rachel's notes from discussions with Chris Budd, Professor of Applied Mathematics at the University of Bath and Principal Investigator of Maths4DL, and early discussions with Rob Tovey, a past member of Maths4DL.

Marianne would like to thank Daniel Nicol for inspiring her AI experimentation with book writing.

This article was produced as part of our collaboration with the Mathematics for Deep Learning (Maths4DL) research programme. Maths4DL brings together researchers from the universities of Bath and Cambridge, and University College London and aims to combine theory, modelling, data and computation to unlock the next generation of deep learning. You can see more content produced with Maths4DL here.