
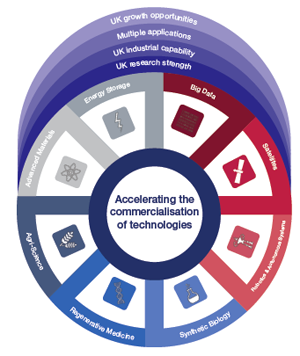
Infographic produced by the UK government.
In 2012 the UK government identified a list of eight great technologies in which it hopes the UK will be a world leader. These were launched in a speech by the former minister for science David Willetts. The speech has led to an industrial strategy report and a flurry of activity on many websites.
It was noticeable that in Willett's speech, in the report, and in the activity it generated, the role of mathematics was only mentioned briefly. This is a symptom of the fact that mathematics still suffers an image problem: it is perceived, widely, to be useless and irrelevant to the modern world. Of course this is very far from the truth, as every (applied) mathematician knows. Indeed mathematics lies at the heart of nearly all of modern technology, as well as much of art and popular culture.
In this article I will attempt to show how maths is essential to the eight great technologies and links them all together. Indeed I would argue that they are eight great mathematical technologies, and that they will lead to many breakthroughs in pure mathematics.
The great eight technologies are:
- Big Data
- Satellites and space
- Robotics and autonomous systems
- Genomics and synthetic biology
- Regenerative medicine
- Agricultural science
- Advanced materials
- Energy and its storage
(More recently, quantum based technology has been added to this list, but we will not go into this here.)
So let's have a closer look at these eight great reasons to do maths.
Big data
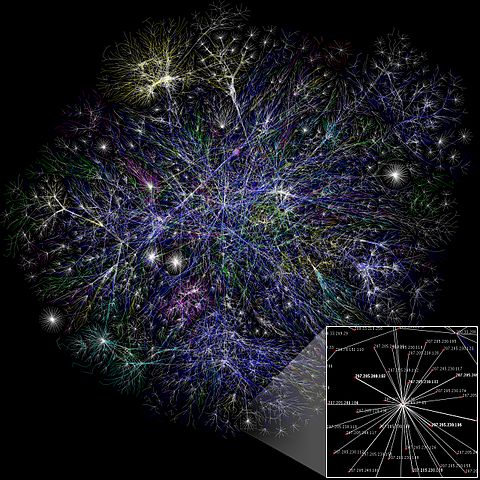
A partial map of the Internet based on 2005 data found on The Opte Project. CC BY 2.5.
One of the biggest challenges that we all face is the challenge of Big Data, and I believe that Big Data impacts hugely on all of the eight great technologies. The reason is simple. We live in the information age, and most of what we do is influenced by our access to massive amounts of data, whether this is through the Internet, on our computers, or on our mobile phones. Access to such a large amount of data leads to large technological and ethical problems. Mathematics can help us with the former, and we should all be aware of the latter.
Many existing mathematical techniques are now finding significant applications in our understanding of Big Data. A key example is the mathematics of network theory. It can be applied to all kinds of networks, be they social networks, social media networks such as Facebook and Twitter, the Internet, transport networks, utility networks, or even the networks of neurons in our brains. Network theory explains the connections between the objects in a network, allows us to search for connections between the data, and can describe the movement of information around a network. In a world full of networks, mathematical tools to understand them are essential.
You can find out more about Big Data and network theory in
Satellites and space
The methods for working with Big Data have natural applications in satellite and space technology. An early success in the data revolution was the use of mathematical error correcting codes in the 1970s to transmit images from distant planets back to Earth without error. With satellites playing a major role in transmitting more and more information, the need for evermore sophisticated mathematical algorithms to keep information accurate and secure will continue to drive mathematical developments.
Mathematics is also playing a major role in helping to understand and control the dynamics of satellite systems. Complex calculations are needed to compute the orbits of satellites over extremely long distances as they leave Earth and explore the distant reaches of the Solar system. (This involves solving differential equations very accurately over long times). Mathematics is also used for the very precise calculations used to orientate the satellites in the Earth's orbit when they are used for GPS navigation.
You can find out more about error correcting codes in
Robotics and autonomous systems

The robots are coming.
Similar numerical methods are used to simulate the movement and control of the robotic systems which form the third of the great technologies. Other applications of mathematics to robotics include machine learning algorithms, pattern recognition techniques, neural networks (artificial imitations of simple nervous systems) and computer vision.
You can find out more about the maths behind machine learning, neural networks, pattern recognition and computer vision in
Genomics and synthetic biology
There is also a natural link between Big Data and genomics and synthetic biology. In particular, this technology relies on understanding how genes and proteins interact. This can be studied by using network theory: the nodes of the networks in this case are genes or proteins and the edges describe allele combinations that control specific phenotypes.
To find out more about the maths behind all things related to genes, read
- Solving the genome puzzle
- It's a match!
- Influenza virus: It's all in the packaging
- Reconstructing the tree of life
- Or any of these articles
Regenerative medicine
Regenerative medicine involves those aspects of tissue engineering and molecular biology that deal with "replacing, engineering or regenerating human cells, tissues or organs to restore or establish normal function". This involves mathematical modelling, and especially the development of novel flexible materials (see also the seventh great technology). Of course mathematics has many other applications to medicine including medical statistics (which has huge relevance to Big Data), modelling and curing cancer and in the various problems arising in medical imaging.
To find out more about the maths behind regenerative medicine, and medicine in general, read
- Modelling cell suicide
- Creating a virtual cancer
- Saving lives: the maths of tomography
- Feeling tense about healing wounds?
- Shaping our bones
- Or any of the articles in our Do you know what's good for you? package.
Agricultural Science

A tomographic reconstruction of a beehive, in which the bees are seen as red dots and honey as yellow. Image from Diagnostic Radioentymology.
Food and beverage processing is the world's largest manufacturing industry and a recent UN forecast has stated that if the population continues to rise at its present rate, then the world food output must increase by 70% by 2050 — a significant challenge to the science of agriculture. Mathematics has many existing, and potential, applications in agri-science and food technology.
The fundamental process of growing (including irrigation), freezing, cold storing, cooking, making, eating and even digesting food are all areas in which the application of areas such as thermodynamics and fluid mechanics can make a very big difference. Similarly, the logistics of feeding a growing world population, which requires food to be packaged, transported and disposed of safely and efficiently, requires the mathematics of optimisation and operational research (and network theory and indeed Big Data again). Even the bee population, which is essential to agriculture, benefits from mathematics. Maths enables researchers to see into bee hives using tomographic X-ray imaging to monitor bees in a non-evasive manner. That way they can hopefully make sure the bee population doesn't decline further than it already has.
To find out more about the maths behind food and its production, see
- Eat, drink and be merry: making it go down well
- Eat, drink and be merry: making sure it's safe
- Helping business make a crust
- Ketchup and traffic jams
Advanced materials
We all rely on materials: natural ones like wood and stone, and also manufactured ones such as steel, glass and concrete. With modern technology, we can design and manufacture meta-materials that have a wide variety of prescribed mechanical, electrical, thermal and other properties.
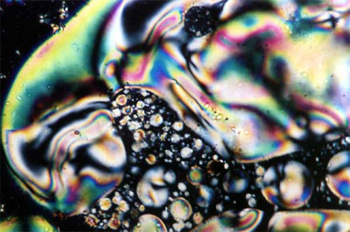
Modelling the complex patterns in liquid crystals requires advanced mathematical methods. Image from Wikimedia Commons, CC BY-SA 3.0.
Some examples of such modern materials are photonic crystals which are used to transmit light with almost zero loss, the complex composites used in aircraft wings, liquid crystals which are used in many displays, and perhaps most intriguingly, the possibility of materials which, in a manner inspired by Harry Potter, confer invisibility on the user. The mathematics needed to design and study such materials is particularly rich and challenging. It can be used to study materials as ancient as rock, or as modern as carbon fibres. It is no coincidence that major growth in modern applied mathematics is in exactly these areas, and I anticipate even more in the future.
To find out more about the maths behind material science, see
- Stretch, but without the wrinkles
- Now you see it, now you don't
- Making a racket: the science of tennis
Energy and its storage
One of the more interesting jobs I have had was as the CEGB research fellow, which was a joint position between the University of Oxford and the (old) Central Electricity Generating Board (now privatised and split up into many different companies). It gave me an a good appreciation of the issues faced by the power generating industry and the importance of mathematics at many levels of this industry.
The job of the electricity supply industry is to supply electricity reliably to us, regardless of the demand. Or more simply put, to keep the lights on. This is not always easy, as too much demand could result in a power cut. An example is the 1990 World Cup semi-final between England and West Germany. At the end of this exciting and emotional match (which England lost on penalties) the power demand surged by 2.8 gigawatts (about 1 million electric kettles), or 11% of the total network demand. Due to good planning by the UK National Grid operators, the lights did stay on, but it was a close-run thing. In contrast, in 2003 a cascade of control system failures of the North-Eastern US power grid lead to a large failure in which the lights did go out. The resulting blackout is estimated to have cost 5 billion dollars.
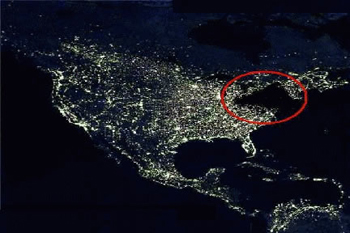
The day the lights did go out in NE America in 2003. The circle shows the blackout region. Image from Datacenterpro.
The annual consumption of electricity in the UK is 300 terawatt-hours, and this electrical power is supplied over a complex network starting, usually, with power being generated at a power station. This is then transmitted over a high voltage network, before being reduced in voltage and distributed to commercial, industrial and residential consumers. To ensure that the lights always stay on, the planners need to solve a large number of equations, described on (another) complex network (with 30 million nodes representing different households, industries and other users of electricity), to work out how much electricity can be generated, distributed and stored. This is not an easy task: electricity must be consumed as soon as it is purchased, it cannot be stored in large quantities and the user has a very low tolerance to interruptions in the supply.
These challenges are going to increase significantly in the future with a greater emphasis on low-carbon generation, a much more distributed supply network, the increase in the use of electric vehicles, an increase in local electricity storage, and the advent of the SMART Grid in which users have greater control over their energy demands and supply more information to the grid company (another example of a Big Data problem). These are all challenges which mathematicians are well placed to address.
To find out more about the maths behind energy, its storage, and its distribution, see
- Renewable energy and telecommunications
- Kissing the frog: a mathematician's guide to mating (yes, it is relevant!).
- Blowin' in the wind
I hope that I have whetted your appetite. The eight great technologies certainly present enormous opportunities for mathematicians in the next fifty years and beyond. I encourage all mathematicians regardless of which country they live in to rise to the challenges presented by these eight great reasons to do mathematics.
About the author

Chris Budd.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin and features in the book 50 Visions of Mathematics ed. Sam Parc.