Maths in a minute: Conway's Game of Life

John Conway's Game of Life is a cellular automaton, which is supposed to produce patterns that resemble living organisms. It was developed by the mathematician John Conway in the 1970s.

The Game of Life is played on an infinite two-dimensional grid of square cells.  A cell that is green is considered to be alive and a cell that is grey is considered to be dead. Every cell interacts with its eight neighbours which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur:

1. Any live cell with fewer than two live neighbours dies (as if caused by underpopulation).
2. Any live cell with two or three live neighbours lives on to the next generation.
3. Any live cell with more than three live neighbours dies (as if by overpopulation).
4. Any dead cell with exactly three live neighbours becomes a live cell (as if by reproduction).

The initial pattern constitutes the seed of the system. The first generation is created by applying the above rules, simultaneously, to every cell in the seed. As with the one-dimensional cellular automata, the rules continue to be applied repeatedly to create further generations. Depending on the seed, very exotic patterns can emerge.

You can explore the Game of Life in the interactivity below, created by our amazing colleague Oscar Gillespie. It starts off with a random pattern of live cells. If you would instead like to choose your own starting arrangement of live cells, click Clear the grid and then click on the individual cells you would like to be live. To run just a single step of the Game of Life, click on Run a generation. To run through many steps, click Run. And to start again, click Stop and then Reset.

Conway's game of life shows that even very simple rules can produce a large variety of different behaviours, including highly organised and very complex ones. What's amazing is this wasn't what Conway set out to show when he designed the game — what he was really after was an infinitely programmable computer. Find out more in our interview with Conway.

Here are some interesting initial patterns to play with:

• The pulsar

  

   

  
   

• A tetromino

  

   

  
   

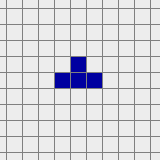
• A diehard

  

   

  
   

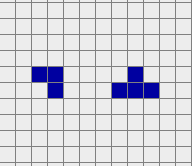
• A glider

  

   

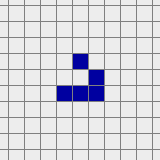
• A gun

  

   

About this article

This article is based on an extract from Cellular automata by Chris Budd. The interactivity was produced by Oscar Gillespie.