An exciting development has occurred in the area of mathematical billiards.

Like pool and snooker, billiards involves balls rolling around on a table. Mathematicians like to think about it because, even though the set-up is simple, all sorts of weird and wonderful things can happen. "You can think of mathematical billiards as a testing ground for exploring what can happen in dynamical systems that appear in real life," says Oscar Bandtlow, one of the mathematicians behind the latest result. "That's why a whole theory of mathematical billiards has been developed. And it still poses questions we haven't been able to answer."

If you've ever played pool or snooker, perhaps in a dimly-lit pub at midnight, you know that physical reality has a hand in the game. Moving balls feel the friction from the table, and eventually trundle to a halt. The table might be wonky and the balls dented. Your own skill at shooting the ball exactly where you want it, especially if you're in a dimly lit pub at midnight, might also be impaired. Or perhaps you never gained that skill in the first place.

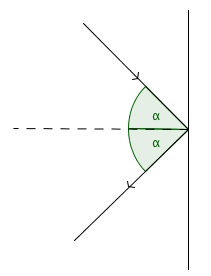
A ball in mathematical bounces off the side of the table in the same way as real balls do, following the law of reflection: the angle of incidence equals the angle of reflection.

Mathematical billiards ignores these physical inconveniences. It imagines the balls as points that don't feel friction, so that once a ball gets going, it will keep moving forever. When a ball meets a side of the table it bounces off like real balls do, leaving at the same angle to the side at which it arrived.

Like real billiard tables, but unlike pool tables, a mathematical billiard table doesn't have pockets a ball can fall into. If a ball rolls into a corner of the table, it is imagined to get stuck there forever. Since mathematicians are usually interested in what happens on the table in the long term, they often ignore this possibility, focussing only on trajectories that never land in a corner and therefore keep going forever.

All or nothing

The question is, what can happen to a mathematical ball once it's been set in motion? If it hits a side of the table straight on, so it meets it at a 90 degree angle, then it'll simply retrace its path until it hits a point on the opposite side, only to retrace its path again. You get a periodic motion, bouncing back and forth between two opposite points forever. With a little more finesse you can also make a ball bounce periodically between three, four, or even more, points on the table's sides.

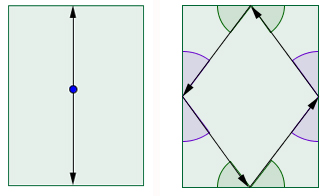
Left: if you shoot a ball so it meets the wall at right angles, it will bounce between opposite points on the table forever. Right: similarly, you can make the ball travel between four points. These are examples of periodic trajectories.

As you'll know from the real-life game, getting a ball to behave periodically is difficult. Most of the time (in fact almost always) when you get a ball moving, the trajectory it'll follow is a lot wilder. The astonishing thing is that, once a trajectory goes wild, it does so completely: given enough time, a non-periodic trajectory will essentially fill up the whole table, coming arbitrarily close to every single point on the table. This is surprising, but there's mathematical proof (see this article for a little more detail).

This leaves us with an all-or-nothing situation. Either a ball's trajectory is totally tame, retracing the same path again and again to eternity, or it ends up going pretty much everywhere. (That's ignoring trajectories that get stuck in corners, as we noted above.)

Billiards on polygons

The all-or-nothing result doesn't only apply to tables with a rectangular shape. You can play mathematical billiards on a square, an equilateral triangle, a regular pentagon, regular hexagon, regular heptagon, etc, and you will always find the same two types of possible behaviour: either the trajectory of a ball is periodic, or it eventually gets as close as you like to every point on the table. In the latter case the trajectory of the ball is said to be dense. (Again, that's ignoring trajectories that end up in a corner.)

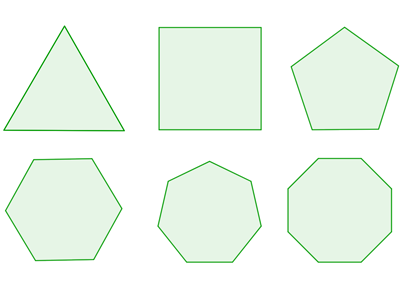
Some regular polygons. Top row: an equilateral triangle, a square and a regular pentagon. Bottom row: a regular hexagon, heptagon and octagon.

This poses a natural question: are there any table shapes where the result doesn't apply? This would mean that a ball can move about in a non-periodic fashion while still leaving out a piece of the table.

The shapes mentioned above are all polygons, that is, closed shapes bounded by bits of straight line. In fact, they are regular polygons whose sides are all the same length. What's more, they don't have any inwards-facing dents, in other words, they are convex (see Wikipedia for a formal definition).

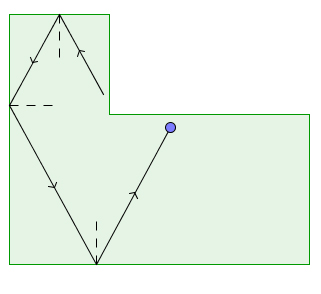
An example of a non-convex polygon. It's got an inward-facing dent, like someone has broken a chunk off a rectangle.

The all-or-nothing result was only shown to hold for regular polygons and a class of very special convex polygons which, like the regular ones, are also highly symmetric. But what about generic convex polygons that aren't quite as special? Does the all-or-nothing result hold for them too? (Regarding non-convex polygons, there are examples of them for which the all-or-nothing result holds and examples where it fails. And anyway, they aren't as nice as convex ones, so we ignore them.)

In 1983 the mathematician G.A. Galperin proved that the answer is no. He showed that, for any number of sides you care to pick, there's a convex polygon with that many sides for which the result fails. For these polygons you can find trajectories that are neither dense nor periodic. It appears, then, that the all-or-nothing result is a feature of only a select and special few.

There was, however, something curious about Galperin's proof of this result. He used the same technique for all polygons with four sides or more, but for polygons with three sides, triangles that is, he had to come up with a different technique. A full 32 years later it became clear that Galperin's reasoning about triangles had indeed been wrong. In 2015 George William Tokarsky published a a very short paper which pointed out a mistake in the part of the proof that applies to triangles. This turned the triangle case into a tantalising tease for mathematicians. Are triangles like all the other polygons, so the all-or-nothing result can fail, or are they somehow special, so the result must always hold?

The new result

That's exactly the question that Bandtlow, together with Wolfram Just and Julia Slipantschuk, was able to answer. The team found a family of triangles on which a mathematical billiard ball can move around in a non-periodic fashion while at the same time missing out a whole chunk of the table. The all-or-nothing result therefore fails for such triangles — in this sense, triangles are no more special than their many-sided cousins.

An example is shown in the image below. The triangle has two equal sides, shown as the two sides that slope upwards. The two angles at the base of the triangles are $\sqrt{3}/6 \pi,$ and the one at the tip is $(1-\sqrt{3}/3)\pi$. As the figure indicates, the trajectory of the ball in this case, shown in blue, misses out the tip of the triangle.

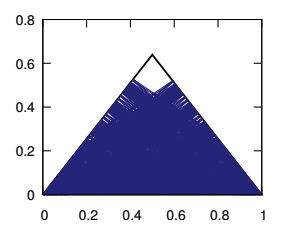
An example of a piece of trajectory in a triangle. It includes 500 bounces off the sides of the triangular table. The trajectory is not periodic and pretty much fills up a large part of the triangle — but it does miss out the tip. Image from Non-periodic not everywhere dense trajectories in triangular billiards, used by permission.

The result closes the gap in the theory of billiards that Tokarsky's proof of Galperin's mistake had opened up.

"We are very pleased to have finally put the case of the triangle to rest," says Bandtlow. "We will now see whether the tools that we and others have developed can answer other open questions in mathematical billiards — and there still are many of them."

Further reading

You may also want to read Chaos on the billiard table and Playing billiards on doughnuts.

About this article

Marianne Freiberger is Editor of Plus. She interviewed Oscar Bandtlow in January 2023.