We're all familiar now with R, the effective reproduction ratio of a disease: the average number of people an infected person goes on to infect. (You can read an introduction to the reproduction ratio here). If R is greater than 1, the number of infected cases grows exponentially, which will cause a large number of deaths for a dangerous disease like COVID-19. When R is less than 1, and stays that way, then the number of new infections becomes progressively smaller and the epidemic comes to an end.

This was the reason countries around the world have locked down: to reduce the effective reproduction ratio R to below 1. While we are often talking about a value of R that gives the average for the whole country, looking at particular locations and particular components of society may give you different values of R. For example, the value of R within care homes and hospitals might be higher than it is in the community.

The danger of combining Rs

You might think that to get the overall value of R, which applies to the community, hospitals and care homes taken together, you simply take the average of the two values. In reality this isn’t the case and leads to a dangerous underestimate of the overall value of R. It can even lead you to assume that the disease is under control when really it is not.

The reason for this is that the populations, people in the community and people in hospitals, are not completely isolated from each other. (To make this discussion simpler, we'll group care homes and hospitals together and refer to them as "hospitals".) People from the community move into hospitals when they get sick, and staff from hospitals (who we include in the hospital population for this discussion) can unwittingly take the virus out into the community. It is this transmission between the two groups that can drive up the overall value of R. This is why we need to be very careful when considering values of R in different settings together.

Here is a simple example. Say the value of R in the community is 2, so on average an infected person in the community infects 2 others in the community, and the value of R in hospitals is 3, so on average an infected person in a hospital infects 3 others in the hospital.

We also need to take into account that there will be contact between the two groups, so say that on average a person in the community also infects 1 person in a hospital (in addition to the 2 people they will infect in the community). Similarly, say a person in a hospital infects 1 person in the community on average (in addition to the 3 people they infect in hospital).

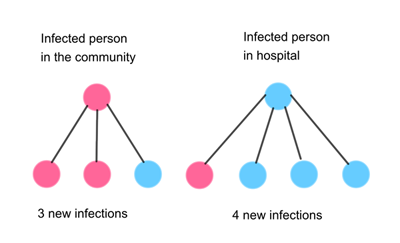
Note: the numbers in this example are not taken from real life and are only used here as an illustration.

Then as you can see from the diagram above, a person in the community and a person in a hospital together infect 7 people. This means there are 7/2=3.5 new infections per person on average for this first round of new infections.

As we continue this, we see that the ratio between new infections and infections at the previous step grows to 25/7=3.57 (see the diagram below). Carrying on further will eventually lead us to an overall value of R of 3.62. Crucially this is higher than any of the individual values of R, which were 2 and 3.

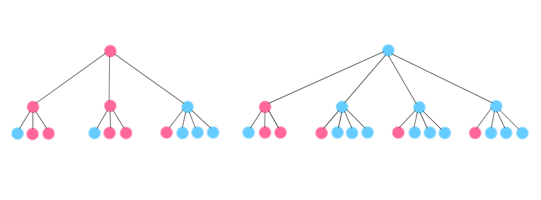
There are 25 new infections (third row of circles) and 7 infections at the previous step (second row of circles), so the ratio is 25/7=3.62.

A false sense of security

The fact that the overall value of R is higher than any of the individual values becomes particularly striking when the individual values are all less than 1. When that is the case, you might think the disease is under control and decide to ease the lockdown. However, the overall value of R may still be greater than 1, leading to renewed exponential growth and a second spike in the epidemic.

Here is an example using more realistic figures. The reproduction ratio for the community in lockdown is now thought to be less than 1 one, say it is 0.8. (You can think of these fractional reproduction ratios in this way: if there are 1000 people with the disease, then on average, they will go on to infect 800 other people.) And the reproduction ratio for infections within hospitals and care homes might be slightly lower, say 0.7. These numbers might lead you to believe that, as they are both under 1 one, we now have the disease under control and begin to return to normal life.

But what about infections between the two groups? A reasonable assumption is that an infection in the community might go on to cause 0.4 new infections in hospital, and an infection in hospital might go on to cause 0.2 new infections in the community. Now we have four numbers for transmission within, and between hospitals and the community:

Transmission within community 0.8	Transmission from hospital to community 0.2
Transmission from community to hospital 0.4	Transmission within hospital 0.7

All these numbers are less than 1, so it might appear as though the disease is now under control. But unfortunately that isn’t the case. The overall value of R for the population is actually about R=1.04 for this example. See the animation below to see the example unfold. It is the flowing of cases between the two settings that leads to the larger value for the overall reproduction ratio, and also tips the balance of where the most infections are, in hospitals or in the community.

What we have illustrated here using specific examples is true in general: the overall reproduction ratio, R, will always be greater than any of the individual reproduction ratios within different population segments. The lesson from this is that even if the disease is under control within a part of the population, or even within each part of the population, the connectivity between them can allow the epidemic to grow.

The maths to work this out involves some undergraduate university concepts from linear algebra, which you can explore in this article.

About this article

Rachel Thomas and Marianne Freiberger are Editors of Plus. This article wad produced with Julia Gog, Professor of Mathematical Biology at the University of Cambridge, as part our collaboration with JUNIPER, the Joint UNIversity Pandemic and Epidemic Response modelling consortium. JUNIPER comprises academics from the universities of Cambridge, Warwick, Bristol, Exeter, Oxford, Manchester, and Lancaster, who are using a range of mathematical and statistical techniques to address pressing question about the control of COVID-19. You can see more content produced with JUNIPER here.

The animation was created by Oscar Gillespie, Web Application Developer for our sister site NRICH.