The shape and fate of the Universe
It's taken humanity a very long time to work out that the Earth is round. This isn't surprising, seeing that we're too small to notice the curvature of the Earth as we walk around on it. To someone as small as us the Earth appears flat and infinite in all directions.
It's easy to make the same mistake when it comes to the shape of the Universe. To us it appears infinite and un-curved. But that's not the only possibility.
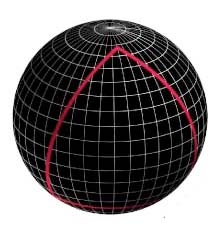
The surface of a sphere is finite, but it doesn't have an edge. The angles of a spherical triangle add up to more than 180 degrees. If the Universe has positive curvature, then its geometry is the 3D analogue of a sphere.
According to Einstein's general theory of relativity massive objects curve space (see here to find out more). If you assume that the Universe is isotropic (looks the same, on average, in every direction in the sky) and homogeneous (looks the same, on average, at every point), and that there is none of that mysterious substance called dark energy, then general relativity tells you that there are only three possibilities for the shape of the Universe, depending on how much matter there is within it.
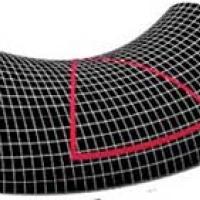
The first possibility is that the density of matter (the average amount of matter per unit volume) is so high, it curves the Universe around on itself to form the 3D analogue of a sphere. This 3D sphere is hard to imagine, but it's easily described mathematically and comes with a positive value for its curvature. (Curvature is a precisely defined mathematical concept, see here to find out more.) If the Universe is indeed positively curved, then it is finite, just like the surface of a sphere is. What is more the gravitational pull exerted by all the mass will eventually stop it from expanding (which it is currently doing) and cause it to contract. Eventually it will end in a big crunch.
One thing that allows you to see whether a given space is positively curved is to draw triangles. If you'd like to travel between two points on a sphere along the shortest route, then you should travel along a great circle: a circle that passes through two opposite points on the sphere. Great circles are the analogues of straight lines on the flat plane. If you draw a triangle whose sides are made from pieces of great circles, you will find that, unlike in flat 2D space, its angles add up to more than 180 degrees.
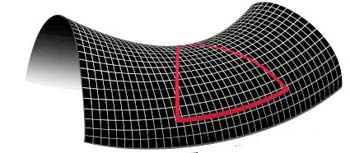
The surface of a saddle. The angles of a triangle drawn on this saddle add up to less than 180 degrees. If the Universe has negative curvature, then its geometry is the 3D analogue of an infinite saddle.
Another possibility is that the density of matter is so low that the curvature of the Universe is negative. In this case, the Universe is the 3D analogue of the surface of a saddle. The angles of a triangle add up to less than 180 degrees and the Universe is infinite. It's hard to visualise this 3D hyperbolic space, but again it's easy to describe it mathematically. As for the ultimate fate of the Universe, there's not enough matter to significantly slow the rate of expansion: ultimately, the Universe will die in a cold and lonely big freeze. (You can find out more about spherical and hyperbolic geometry in this Plus article.)
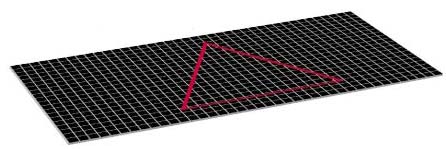
A piece of the flat plane. The angles of a triangle drawn on this plane add up to exactly 180 degrees. If the Universe has zero curvature, then its geometry is the ordinary 3D space we learn about at school.
Finally, it could be that there's just enough matter for the Universe to have zero curvature. Angles of triangles add up to exactly 180 degrees and the Universe is infinite. If this is the case then it may be that matter can slow the rate of expansion, but it'll never be able to bring it down to zero. The Universe will also expire in a big freeze.
Observations of the cosmic microwave background (the left-over radiation from the Big Bang) suggest that the Universe is indeed flat, or at least very nearly so. This would imply eternal expansion, at least if the assumptions above are true.
But are they? The first is that general relativity is true. The theory has been tested many times and has always stood up to the tests admirably, so physicists on the whole take it to be true (though there are dissenters, see here). Another assumption is that the Universe is isotropic, that is, as we look in the various directions in the sky, no direction stands out over an other, they are all the same, on average. This idea may seem strange at first, since the world definitely looks different in different directions. However, this assumption refers to the average look over large volumes of space. Based on current observations, this average really is the same everywhere, so the Universe is indeed likely to be isotropic. One you accept isotropy, then homogeneity can only fail if you accept that our location in space is somehow special, an idea that physicists reject.
The only assumption that isn't true is the one asserting that there should be no dark energy. Dark energy does exist and its existence makes the relationship between the geometry of the Universe and its fate a little more complex. However, it is still is the case that a flat Universe will expand forever. Big freeze it is then.