Content about “

editorial

”

This issue of Plus is devoted to the winning entries of the Plus New Writers Award 2006.

Learn about the aerodynamics of footballs and perfect your free kick.

Time series plot 6

This plot shows the orbit of zero for iteration of x² + 0.2 . You can see that after some iterations the points in the orbits remain almost the same.

Time series plot 5

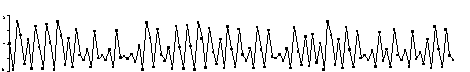
This plot shows the orbit of zero for iteration of x² - 1.85. The orbit does not settle down, it is chaotic.

Time series plot 4

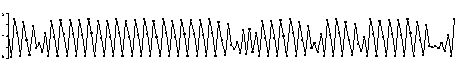
This plot shows the orbit of zero for iteration of x² - 1.8. Even though the orbit is close to a 3-cycle for periods of time, it never settles down completely. It is chaotic.

Time series plot 3

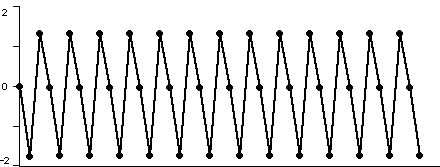
This plot shows the orbit of zero for iteration of x² - 1.75. It tends to a cycle of period 3.

Return to the article

Time series plot 2

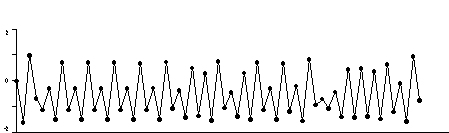
This plot shows the orbit of zero for iteration of x² - 1.6. The orbit does not settle down, it is chaotic.

Time series plot 1

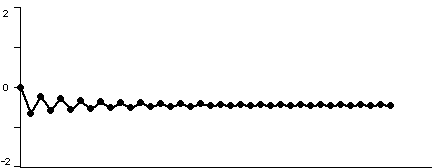
This plot shows the orbit of 0 for iteration of x² - 0.65 . You can see that after some iterations the points in the orbits remain almost the same.

The filled Julia set of x² + 0

To work out the filled Julia set of x² + 0 = x² we need to look at all the points on the complex plane and decide whether or not their orbits escape to infinity. Those whose orbit doesn't escape are part of the filled Julia set.

A brief introduction to complex numbers

Complex numbers are based on the number i which is defined to be the square root of -1, so i times i equals -1. This number isn't a real number, in other words it does not appear on the usual number line. For this reason it is called an imaginary number, a slightly contentious name. Now any complex number is of the form a + ib, where a and b are ordinary real numbers.