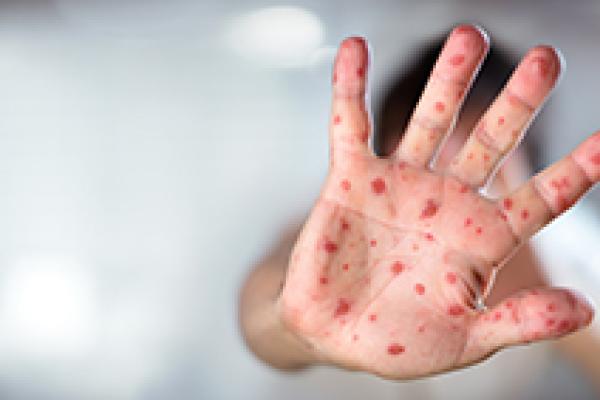
Measles cases on the rise: Why this is worrying and what we can do
We look at the recent rise in measles cases, why it has led to a national health incident being declared, and what can be done to avert the threat.

We look at the recent rise in measles cases, why it has led to a national health incident being declared, and what can be done to avert the threat.

From tiling bathrooms to fooling cancer cells, and from new insights in topology to bringing research into the classroom — we hope you enjoy our April round-up!

We know climate change can impact our lives through weather events and food security, but it can also impact on the spread of diseases. We talk to Helena Stage from the University of Bristol to find out more.

How does maths help in tackling infectious diseases? Join Julia Gog to find out in this series of videos and articles, and have a go at modelling diseases yourself!





With just some simple arithmetic, you can build a basic mathematical model of how a disease might spread. Julia Gog explains how, and there's also some Lego action...

You can explore how we might extend our model but running your own epidemic with our Lucky Dip interactivity. Follow along with Julia as she paves the way to a model that is very similar to the mathematics disease modellers use every day.

In Part 3 Julia refines our model to use one of the most important numbers in disease modelling. And there's a chance for you to explore its meaning using a new interactivity.

In the final Part we explore what other aspects we need to consider to make a model more realistic. There's an interactivity that allows you to party, commute, and visit friends and we find out more about what life as a research is like from Julia.

In this final part, you can meet the researchers themselves and find out about the real research questions that Julia and some of her colleagues are working on!
The reproduction ratio, R, is one of the most important numbers in epidemiology. Find out what it means in this very easy introduction.