
What is symplectic geometry?
Recently we came across what's known as symplectic geometry and it had us fascinated. It's different from the geometry we learn at school, and for good reason. Its purpose, when it was first invented, was to capture the essence of something that, at first sight, is far removed from geometry: the behaviour of dynamical systems, such as a swinging pendulum or a marble rolling down a track. Here's a brief introduction.
All about area
Symplectic geometry involves objects known as symplectic manifolds. Generally, a manifold is a space that locally looks like the ordinary Euclidean space we are used to from school geometry, but globally may have a very different structure. An example is our planet. Because we are too small to detect the Earth's curvature, the local patch of Earth we are standing on appears to us as a flat Euclidean plane. Seen as a whole, however, the Earth is anything but flat: it's a sphere. Spheres are examples of two-dimensional manifolds.

The Earth is an example of a two-dimensional manifold.
When working with a manifold it's natural to want to impose a geometric structure on it — to define ways of measuring lengths and angles, for example. This gives rise to an area of maths called Riemannian geometry, named after the 19th century mathematician Bernhard Riemann.
Symplectic geometry focuses on the geometry of area, rather than length and angles. A symplectic manifold, even if it has more dimensions than we can visualise, comes with a clearly defined, generalised notion of area.
From dynamics to geometry
Symplectic geometry was to a large part inspired by a version of mechanics formulated in 1833 by the mathematician and physicist William Rowan Hamilton. While Hamiltonian mechanics can describe the same physical phenomena as the versions developed by Isaac Newton and Joseph-Louis Lagrange before him, it has certain advantages over both, which is why it attracted people's interest.
Like Newtonian and Lagrangian mechanics, Hamiltonian mechanics can be used to describe the behaviour of dynamical systems. Imagine, for example, a marble rolling around a circular track. To describe the state of this system at a given moment in time, you need to know the marble's current position on the track and its speed, or, alternatively, its momentum. Momentum is the product of an object's speed and its mass which, loosely speaking, measures how hard it would be to bring the object to a stand-still.
To keep track of both position and momentum at once, you might visualise the marble's journey on a vertical cylinder instead of a circle. The marble's journey around the track is represented by a path winding around the girth of the cylinder. Changes in momentum are reflected by the path spiralling up the cylinder (when the marble accelerates) or down it (when it slows down).
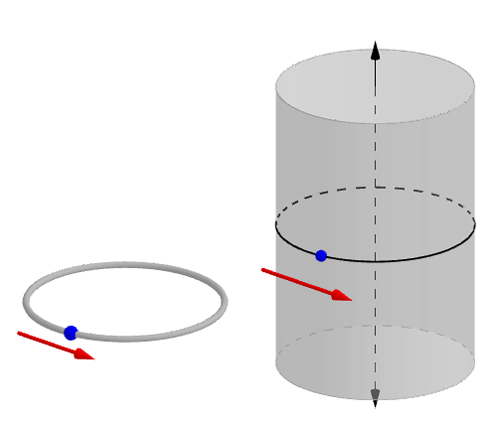
Left: a marble rolling on a circular track. Right: the phase space of the system, which is a cylinder. Every point on the cylinder corresponds to a possible state of the system. The height of the point reflects the momentum of the marble for that state, and the location of the point around a horizontal circle the location for that state of the marble on the track.
In fact, the cylinder represents all the possible states of the system — all possible combinations of position and momentum — at the same time. Each state corresponds to a point on the cylinder's surface and vice versa. It is what mathematicians call the phase space of our dynamical system. Since a cylinder is a geometric shape, in fact it's a simple example of a manifold, we have now entered the world of geometry.
Going symplectic
Hamilton's equations of motion can be used to predict the motion of the marble on the track. As the marble moves, its cousin on the cylinder also moves, reflecting the marble's change in momentum and location.
A patch on the cylinder's surface is made up of many points, each corresponding to a possible state of the dynamical system. Since the equation of motion predicts how each state will evolve over time, the equation induces what you might call a flow on the cylinder. The patch on the cylinder's surface is moved around by this flow in a way that reflects how the states that sit within the patch evolve. And while the patch may change shape as it moves along, Hamilton's equations imply that its area will always remain the same.
Something similar is true for all sorts of dynamical systems, even ones that are much more complicated than our example. The phase space of such a system forms a manifold. You may need more than one coordinate to describe the positions and momenta of objects in the system (in three-dimensional space, for example, you need three coordinates each) so the manifold won't necessarily be a two-dimensional surface like the cylinder. However, it is possible to define a measure of size with reference to the position and momentum pair which generalises the notion of area in the two-dimensional case. This measure of size is the generalised notion of area mentioned above, and it is preserved by the flow induced by the dynamical system.
Beyond Hamilton
The shape of the symplectic manifold that embodies the phase space of a Hamiltonian system can tell you a lot about the possible behaviours of the system itself, and that's where the interest in symplectic manifolds originated. But since symplectic manifolds can also be defined and studied without reference to Hamiltonian systems, this now presents a field of research in its own right. It lies at the intersection of various other disciplines, drawing on algebraic geometry (which investigates geometric shapes defined by equations), topology, and representation theory (find out more here). There are also deep connections to theoretical physics through mirror symmetry, a notion that comes up in string theory.
For a more technical introduction to symplectic geometry, see Wikipedia.
About this article
This article is based on a piece we wrote for the website of the Faculty of Mathematics at the University of Cambridge. We would like to thank Ivan Smith, Professor of Geometry at the University of Cambridge, for his help. Below you can see a video interview with Smith, filmed at the International Congress of Mathematicians 2018, where he was an invited speaker.
Marianne Freiberger is Editor of Plus.