
Why is the Earth a magnet?
Good question. The Earth is indeed a magnet, although it's very weak. A good fridge magnet is over 200 times stronger. As a very crude approximation, you can imagine the Earth's magnetic field to be that of a bar magnet at the centre of the Earth, which is roughly aligned with the axis the Earth spins around, but tilted by about 11 degrees. The points where the North-South axis of this magnet intersects the Earth's surface are called the geomagnetic poles. Because of the tilt of the magnet's axis, the geomagnetic poles are not in the same places as the geographic poles.
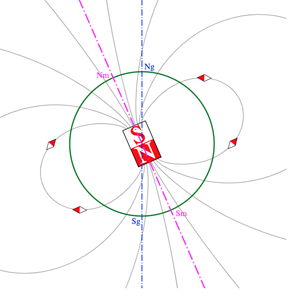
This diagram illustrates how the Earth's magnetic field can be approximated by that of a bar magnet. The blue axis represents the Earth's rotational axis with the geographic North and South poles at top and bottom. The pink line represents the orientation of the bar magnet with North and South geomagnetic poles. Figure: JrPole, CC BY-SA 3.0.
The South pole of our imagined bar magnet points in the northerly direction on Earth, while its North pole points in a Southerly direction. This is why the geomagnetic pole in the Earth's North actually corresponds to South in the magnetic sense, and the geomagnetic pole in the Earth's South corresponds to North in the magnetic sense.
This is not yet all as far as the poles are concerned. Because the picture of the bar magnet is only an approximation, the North and South geomagnetic poles are also only approximations of the true poles of the Earth's magnetic field. The true poles are the points on Earth where the magnetic field lines point vertically down. Unlike the geographic and geomagnetic poles, the true magnetic poles are not directly opposite each other. They also move around independently of each other. At the moment, it seems the magnetic pole in the North is moving in a north-westerly direction by about 45km a year. What's more, geological records show that the Earth's magnetic field can even flip around. The last time this happened was about 780,000 years ago.
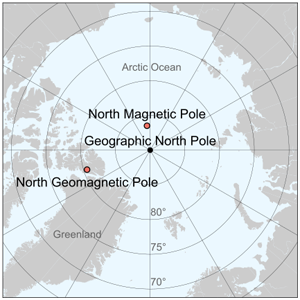
Locations of the North magnetic pole and the North geomagnetic pole in 2017, shown on a map together with the geographic North pole. Figure: Cavit, CC BY-SA 4.0.
Where does the magnetic field come from?
Nobody knows for sure, but the accepted theory is that the Earth acts like a dynamo. To understand how this works, first remember some physics you might have learnt at school. When you move a conducting material through a magnetic field, then this induces an electric current in the material. This process is known as electromagnetic induction and is also what happens in the kind of dynamo that is used to power bicycle lights. Conversely, an electric current can generate a magnetic field.
The Earth has a solid inner core which is roughly the size of the Moon but around as hot as the surface of the Sun. The inner core is surrounded by a liquid outer core mostly made up of molten iron, which can conduct electricity. Various processes that occur within these deep layers of the Earth cause the liquid outer core to be in constant motion (the liquid convects).
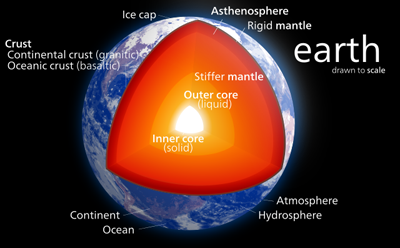
The internal structure of the Earth. Figure: Kelvinsong, CC BY-SA 3.0.
To understand dynamo theory imagine that in the beginning there was a magnetic field. Don't worry about where this field came from (it could have been caused by solar wind for example) because we only need it to kick start the Earth dynamo. Since the conducting liquid outer core was in motion within the magnetic field, electric currents were generated in the liquid. Because of the rotation of the Earth, such currents are organised in spiralling columns.
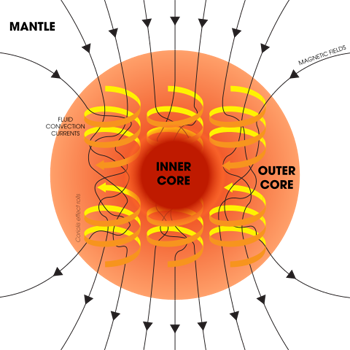
A diagram showing the relationship between the motion of conducting fluid (organised into rolls by the Earth's rotation) and the magnetic field that the motion generates. Figure: Andrew Z. Colvin, CC BY-SA 4.0.
The currents in turn generated their own magnetic field, which amplified the original magnetic field and evolved into the kind of magnetic field we see today. Because the liquid outer core keeps convecting, currents keep being generated, so the magnetic field can sustain itself over extremely long periods of time. And because the motion of the liquid is complex and variable, so is the magnetic field.
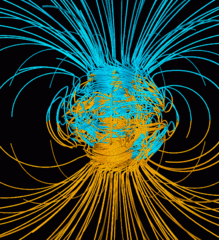
Computer simulation of the Earth's field. The lines represent magnetic field lines, blue when the field points towards the center and yellow when away. The dense clusters of lines are within Earth's core. Image courtesy NASA.
Old Earth, new science
This gives an (extremely rough) outline of dynamo theory, but the details are far from simple. To really understand what's going on, to calculate the exact shape of the Earth's magnetic field and predict how it's going to evolve, you need to combine the mathematics that describes the motion of fluids (the Navier-Stokes equations) with the mathematics that describes electromagnetism (Maxwell's equations). People have done that and come up with a theory that goes by the beautiful name of magnetohydrodynamics. (You can read about the central equations of this theory on Wikipedia.)
The theory can be used, not only to describe Earth's magnetic field, but also magnetic fields generated by other planets and stars. Understanding these magnetic fields can tell us a lot about the material a celestial body is made of and how it interacts with its environment. Magnetohydrodynamics is also useful back here on Earth: it could help us produce liquid metal batteries and cleaner power plants, and even help clinicians direct a cancer drug towards a tumour using magnetic fields.
There is a catch, however. The central equations of magnetohydrodynamics are generally incredibly difficult to solve. To solve them you either need to simplify them or rely on sophisticated methods that deliver approximate solutions and often require vast amounts of computing power. A lot of active research is currently going into advancing the theory and improving the methods for finding solutions, while taking account of observations, for example of the magnetic fields of planets and stars other than our own.
At the time of writing this article, top researchers in the field are gathered together at the Isaac Newton Institute (INI) in Cambridge. The INI is a world-leading research centre for the mathematical sciences and the current research programme on dynamo theory aims to give the field a significant push forward. To find out more about what people are doing at the programme see this article.
About this article
Marianne Freiberger is Editor of Plus.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
