Imagine you could look at a process in the world around you and immediately write down an equation that describes it. Not only would you never again fail a physics exam, you'd also gain near-instant power to make spectacular advances in science. Looking at medical scans, for example, you might find an equation that gives insight into what is happening inside a person's body, which might then help you cure a disease.

We humans don't have this equation-spotting ability, and we never will. Even physics equations basic enough to be taught at school, such as Newton's second law of motion, took millennia to be discovered. There are exciting new developments in machine learning, however, which mean that at some point artificial intelligence may be able to help us discover the equations that govern real-life processes.

"[We are thinking about whether] we can teach machine learning algorithms to directly go from video to being able to give us a first view of what the governing equation might be," says Nathan Kutz, Professor of Applied Mathematics and Electrical and Computer Engineering at the University of Washington and Director of the AI Institute in Dynamic Systems. "This is GoPro physics. You take a little camera, film some [process of interest], and give the video feed directly to an algorithm for it to come back and say: this is what I think the physics are."

Feeding AI with maths

Machine learning algorithms are expert pattern spotters. The algorithm behind ChatGPT, for example, has been trained on a huge dataset of text, including webpages and books. Looking through this vast amount of data, the algorithm spotted patterns and connections humans would not be able to find. When you ask it a question or give it a task, ChatGPT uses its knowledge of these connections to put together a (sometimes) meaningful output. Kutz for example uses it to help him write computer code. (For more detail on how machine learning works see this article.)

GoPro physics.

In the "GoPro physics" algorithms Kutz is talking about, called sparse identification of non-linear dynamics algorithms or (SINDY), this pattern spotting ability is enhanced with important mathematical tools that capture an essential part of physics. Any physical process we might be interested in always involves some form of change. A planet in its orbit changes its position in space over time, a growing plant changes its size over time, and the neurons in our brain change their firing patterns over time.

The changes that define physical systems are captured mathematically by differential equations. These describe the relationships between the variables involved (which could be the position, size, or intensity of something, for example) and the rates at which these variables are changing. Such differential equations are usually made up of components (functions) of a form familiar from maths textbooks - things like 5x, x² or sin(x). For examples of important differential equations, you might want to look at Newton's second law of motion, Maxwell's equation for electromagnetism, or the Navier-Stokes equations which describe how fluids flow.

SINDY is equipped from the outset with ways of working out rates of change from looking at how things change in a video of a physical process. They are also given a vast library of mathematical functions that could combine to form the differential equation that describes the system. The idea is that, with its superhuman ability to spot connections, the algorithm can then go ahead and find the differential equation that best describes the data from the video by looking at combinations of candidate component functions. This could result in some gruesomely unwieldy equation, but the algorithm is given another important directive: to look for the simplest differential equation that fits the data.

There is good justification for going for the most parsimonious representation of a system – all the important equations humans have found to describe physics are astonishingly simple. "It's remarkable that all of the physics that we observe today [is] encoded in very compact representations through governing equations," says Kutz.

Proof of concept: The pendulum

SINDY is still in its infancy but it's had one remarkable success. By looking at video of a swinging pendulum an algorithm has been able to independently come up with its governing equation (which you can admire in the box). This might not seem like a major achievement, after all we have known this equation for a long time, but it's an important sanity check.

The pendulum

The differential equation for the motion of a simple pendulum is $$\frac{d^2 \theta}{dt^2}+\frac{g}{l}sin(\theta)=0,$$ where $\theta$ is the angle with the vertical, $g$ is the strength of gravitational field, and $l$ is the length of the chord the pendulum is swinging from.

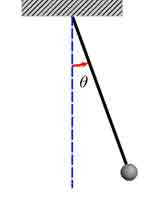
Image: Ruryk, CC BY-SA 3.0 DEED.

A simple pendulum is an idealisation of a real pendulum. To find out what this means, see Wikipedia.

There are in fact two interesting things to note about the algorithm's feat. The first is of a mathematical nature: the algorithm managed, all by itself, to find the correct variable to use when representing the system. When you look at the kind of pendulum involved here — a weight hanging from a fixed support swinging back and forth under the influence of gravity — you might think that the equation's solution should directly provide the trajectory of the weight. It turns out, though, that to get a nice equation you can work with, it's better to phrase the equation in terms of the angle the pendulum makes with the vertical ($\theta$ in the equation). From this you can then work out the trajectory of the weight, should you want to.

"This is how we typically represent the pendulum, in terms of the angle of the motion," says Kutz. "This has been known for a long time, all the way back to the time of Galileo, but it took a long time to even get that understanding. But [the algorithm] discovers this directly from the video [and then comes up with the correct equation]."

The other interesting aspect involves the messiness of reality. The algorithm was able to distinguish between the motion of the pendulum and all the other things that went on in the video. "[One thing is the lighting]," says Kutz. "There's the pendulum there but there's also a light in the room reflecting electromagnetic energy back and also creating shading effects. So you have to work hard to disentangle these things. For the pendulum we figured out how to do that. The machine learning disentangles this for you and figures out to ignore [the lighting] in favour of the simple model of the pendulum. The hope is that we can make this platform much more robust, stable and broader so that we can film much more diverse phenomena."

From worms to the stars?

It's a long way from a pendulum to new physics. But if the SINDY approach proves a success, then there's a lot of fertile ground for the algorithms to work on. On the one end of the spectrum there are astronomy and cosmology, which are undergoing a data revolution as telescopes become ever more powerful. Looking through such data, a SINDY algorithm might, for example, find the tweaks we might need to make to Einstein's general theory of relativity to understand all that is going on in the cosmos.

On another end of the spectrum there are the processes that go on in the brains of Earth-dwelling creatures. Ryan Raut, a postdoctoral researcher working with Kutz, has been working on imaging the brain of a mouse running on a treadmill. Such imaging involves taking a range of measurements of different quantities and then constructing an image from those. But amazingly, as Raut showed, all these measurements can be expressed in terms of just a few variables — and all you really need to do to reconstruct these is look at the mouse's eyes. "You can look at the pupil dilation of the mouse, and how the pupils are moving, and from that you can construct the whole brain image," says Kutz.

This simplicity suggests that there may be a relatively simple underlying mathematical model that describes the mouse's brain activity — a governing equation of the mouse's brain. And if this exists then a SINDY algorithm may be able to spot it from brain imaging. "This is what's exciting, we finally have a tool to maybe go after [governing equations] in neuroscience."

C. elegans worm. Image: Bob Goldstein, CC BY-SA 3.0 DEED.

It's dangerous, of course, to extrapolate from mice to people, but it's tempting to wonder whether such a governing equation might also exist for the human brain. If that's the case, then it may give insight into the many mysteries we still don't understand: how we switch between states of consciousness and modes of thinking, how the brain and mind control the body, and what is behind diseases such as Alzheimer's and Parkinson's.

Kutz admits that the first success of machine learning algorithms in neuroscience is likely to come, not from mice or people, but from a worm by the name of C. elegans. It is one of the simplest organisms with a nervous system, consisting of only 302 neurons, and therefore perfect for study. "I think we're going to be able to solve that one. Within a shorter space of time we are going to be able to say: here's how the worm controls itself, makes transitions, and modulates its behaviour."

If this application to neuroscience sounds frightening, it's worth pointing out that the algorithms are merely tools for doing something that humans have been doing for a very long time — fitting equations to data — only they're much better at it than we are. Every new tool that we've ever invented, from the axe to gene editing, has come with a potential for danger. The question for us is how to minimise the danger while maximising the potential for good.

This potential, Kutz thinks, is overwhelming. "I'm excited by this hybrid modelling paradigm, making maximal use of machine learning and maximal use of our physics knowledge. What we're doing is leveraging the entire construct of humanity of science and mathematics and combining it with these machine learning tools which have exceptional learning capabilities. This might give us a massive acceleration of discovery and learning."

About this article

Nathan Kutz

J. Nathan Kutz is Professor of Applied Mathematics and Electrical and Computer Engineering at the University of Washington and Director of the AI Institute in Dynamic Systems.

Marianne Freiberger, Editor of Plus, met Kutz at the Dynamics, data and deep learning conference which took place in Bristol in March 2024. The conference was organised by the maths4DL research group.

This content is part of our collaboration with the Mathematics for Deep Learning (Maths4DL) research programme, which brings together researchers from the universities of Bath and Cambridge, and University College London. Maths4DL aims to combine theory, modelling, data and computation to unlock the next generation of deep learning. You can see more content produced with Maths4DL here.