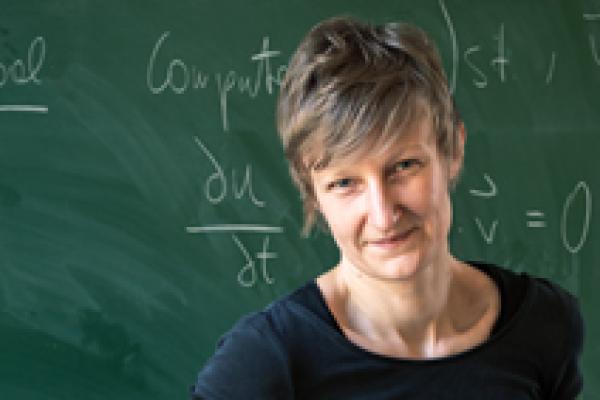The University of Cambridge – the home of Plus

University of Cambridge logo

Plus is based at the Centre for Mathematical Sciences at the University of Cambridge. We are very fortunate to work with many brilliant colleagues in the Maths Faculty, you will find the content we have produced with them below.

 

 

Collection

Women of mathematics

Celebrate female mathematicians with this selection of interviews and videos, which accompany the Women of Mathematics photo exhibition.
Article

Women of mathematics: Holly Krieger

Holly Krieger works in dynamical systems theory, in particular on chaotic systems. Some of her greatest mathematical moments have come from teaching students.
Article

Women of mathematics: Julia Gog

Julia Gog is a mathematical biologist, helping to understand how infectious diseases spread. One of her favourite eureka moments came while she was playing a computer game.
Article

Women of mathematics: Anne-Christine Davis

Anne-Christine Davis is a professor of theoretical physics whose long career has seen attitudes towards women change for the better. She had to put up with quite a lot at the start.
Article

Women of mathematics: Natalia Berloff

Natalia Berloff is a professor of applied mathematics. It was a problem in network theory that lured her into the exciting world of maths when she was ten years old.
Article

Tricky teacups

One of our favourite problems from our sister site NRICH opens a door to the world of combinatorics and symmetry.
Collection

Who's watching: Context is everything

Imagine your weight depended on the colour of your underwear! Something quite similar may be happening when you are measuring things in quantum physics. Find out more here...
Displaying 97 - 108 of 158
Subscribe to University of Cambridge