How to tame uncertainty

Would you put your life in the hands of a mathematical model? If you remember the 2008 financial fiasco, then your answer might well be "no". Mathematical models, delivering false predictions, were widely blamed for the disaster.

Yet, in truth, you are relying on mathematical models many times every day. Whether it's the car you drive to work or the bridge you cross on the way, many of the devices and structures you use have been designed using mathematical models — and the design process includes assessing their safety.

The science of uncertainty quantification, measuring the uncertainty involved in the predictions of mathematical models, plays a hugely important role in all our lives, even if we're not aware of it. But how does it work?

What is a model?

To find out, you first need to understand what a mathematical model is. It's neither a physical object nor a particularly good-looking formula, but consists of a set of equations that describes a (often physical) process: the evolution of the weather, for example, or the flow of air around an aircraft wing. There are plenty of descriptions of mathematical models on Plus, but for a very simple example, think of a ball being rolled along the ground. To a first approximation, its behaviour is described by Newton's second law of motion $f=ma$: the force $f$ of the roll equals the ball's mass, $m$, times its acceleration, $a$.

Such a model can be used to simulate the process in question and make predictions about it: tomorrow's weather, the performance of the air craft wing under various conditions, or the speed of the ball. Apart from seeing into the future, mathematical models allow us to test the design of a product without physically having to build it, crash it, heat it up, or whatever else might be relevant to its useability and safety.

"In the finance sector, in manufacturing, in weather and climate forecasting, mathematical models are just there behind the scenes, informing lots of things we do and take for granted," says Catherine Powell from the University of Manchester, the co-organiser of a recent programme on uncertainty quantification at the Isaac Newton Institute in Cambridge. "Without modelling our lives would be very different."

Model uncertainty

The first step in modelling a process mathematically is to write down the equations you think best describe the process. "Usually we use all the knowledge we have, including any available data, to write down those equations," says Powell. "But no model is exact, every model is an approximation of the real world. There's always an error in going from the truth to a model." As far as our ball is concerned, our simple model above doesn't describe reality with 100% accuracy, for example because it ignores the effect of friction.

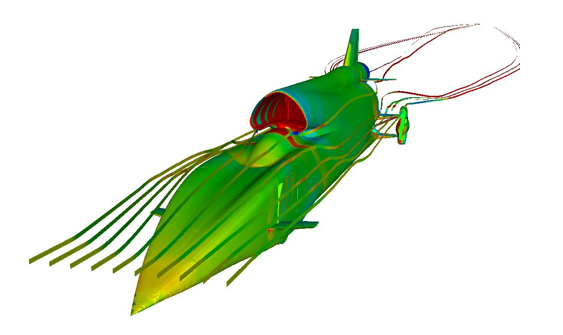
This image is the result of a mathematical model of airflow around Bloodhound SSC, a car built to break the land speed record. It shows pressure contours and streamlines around the car. Find out more here.

That's one source of uncertainty in mathematical modelling: even if you do your best to include all you know in your model, you can never be completely sure that it accurately describes reality. Choosing an unsuitable model, and then confusing it with reality, is a common error in modelling. It's partly what caused the financial crash in 2008.

Approximation uncertainty

Once you have written down your equations, you need to solve them in order to get your predictions. The solution of our simple model for the motion of the ball stares you right in the face: $a=f/m$. This tells you how a ball with mass $m$ will accelerate in response to a force $f$ (ignoring friction). Generally, though, things aren't that easy. "Most models of complex situations, such as modelling the weather or climate change, are every complex and can't be solved by hand," explains Powell. "So we need to try and understand whether we can approximate solutions using algorithms, also called numerical methods."

This is a second source of uncertainty in mathematical modelling: any approximation, by definition, comes with an error. "This is [what] the field of numerical analysis does," says Powell, herself an a numerical analyst. "Trying to make statements about errors associated with numerical algorithms without necessarily knowing what the true solution to your problem is."

Input uncertainty

So far we have ignored the small matter of inputs to the model. To predict the motion of the ball in our example, you need to know the force of the initial roll and the ball's mass. When it comes to weather, to predict what is going to happen tomorrow, you need know today's initial conditions: temperature and pressure, for example. If your model describes a process that changes over space, such as the change of temperature inside a container, you might also need boundary conditions: the temperature of the container itself.

In many real-life situations the values of the inputs of a model are hard to come by. "In engineering problems, for example, we often don't know what all the inputs are," says Powell. "We might have some measurements that give us informed guesses, but there will typically be uncertainty about them." For example, in modelling the flow of groundwater in a particular geological location, an important input parameter is the permeability of the rock at each point of the area you're interested in. You can often only measure permeability by drilling boreholes. Boreholes are expensive, though, so you end up with just a few measurements from which to infer the permeability throughout the area.

This is a third source of uncertainty in mathematical modelling: you can't always be sure what the values of all the inputs of a model are. The famous butterfly effect can inflate this uncertainty beyond all bounds. A small error in the input values can snowball to such an extent that the prediction of your model misses reality by miles. This is a major problem in weather forecasting (find out more here).

We've now identified three major sources of uncertainty in mathematical modelling: model uncertainty, approximation uncertainty and input uncertainty. The question now is how to estimate the uncertainty. That's what we'll do next.

About this article

Catherine Powell.

Catherine Powell is a Reader in Applied Mathematics at the University of Manchester, specialising in numerical analysis. She is an associate editor for the SIAM/ASA journal on Uncertainty Quantification and currently co-runs a network called Models to decisions, tackling decision making under uncertainty.

Masoumeh Dashti.

Masoumeh Dashti is a Lecturer in Mathematics at the University of Sussex, working in Bayesian inverse problems.

Marianne Freiberger is Editor of Plus. She interviewed Dashti and Powell in June 2018 after having met them at the LMS Women in Mathematics Day at the Isaac Newton Institute in Cambridge.