This article describes the moduli space of Riemann surfaces of genus 1. To find out what these are, see the previous part of this article.

Our quest is to understand the entire universe of Riemann tori, where isomorphic Riemann tori are considered to be the same. What we would like, ideally, is some sort of a map to help us navigate this universe. This would be a higher level map than the kind of map we might use to describe a single shape, such as an individual torus. On our universe map, each point would correspond to a Riemann torus. Moving around the map would mean visiting different Riemann tori along the way and getting some information on how they morph into each other as we go.

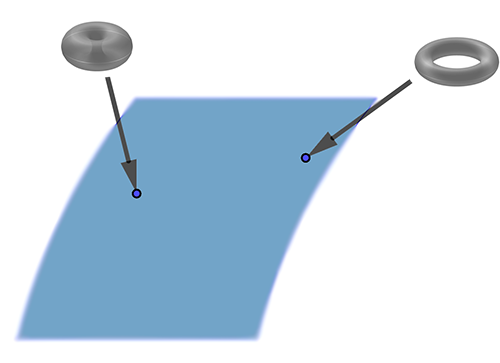
We're looking for a map of the universe of Riemann tori. Each point on the map would correspond to a particular Riemann torus and as you move around on the map you visit many different Riemann tori (where different means not isomorphic.)

Such a universe map is provided by something called the moduli space of Riemann tori. This is what we will construct now, and again we will do this on the level of the lattices that define Riemann tori.

If we consider isomorphic lattices to be the same, then it turns out that we only need one arrow (one complex number) to describe a lattice. That's because given any lattice, it's possible to rotate and scale it in such a way that one of the two arrows that defines it points due East and has length 1, and so that the second arrow points into the upper part of the complex plane (the upper half plane).

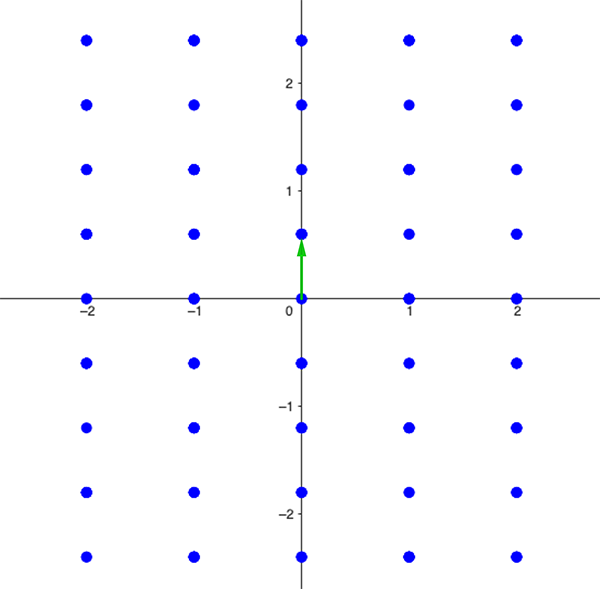
Lattice 3. It comes from lattice 1 (see the previous part of this article) by scaling so that the arrow pointing east has length 1. It is isomorphic to both lattice 1 and lattice 2. The isomorphism class of the three lattices is defined by the single green arrow in this picture (as the other arrow has been set to 1).

It is this second arrow that now uniquely identifies our lattice (and all the ones isomorphic to it). This is a promising approach to creating a map of the universe of all lattices. Every point on our potential map (the upper half plane) can be seen as the end point of an arrow that uniquely determines a lattice. As we move around the upper half plane, we therefore visit all kinds of different lattices.

However, it turns out that, as a map of the lattice universe, the upper half plane overshoots the mark. That's because it's possible for two arrows to define the same lattice. If we visit both their endpoints on a journey through the upper half plane, then we have visited the same lattice twice. Below is an example of two arrows defining the same lattice.

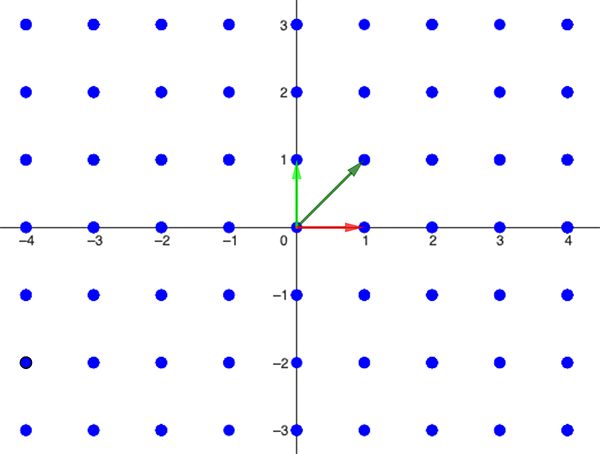
The light green arrow defines the same lattice as the dark green arrow.

We're now in a situation very similar to the one above, where we "unfolded" a torus to give a tiling of the complex plane. This was a great way of keeping track of paths on the torus, but as a flattened out map of the torus, the tiling overshot the mark. To get such a map it was sufficient to consider just one of the rectangles.

It turns out that the upper half plane can also be divided up into regions (called fundamental domains), which can each serve as a map of our universe of lattices. And just as our torus came from gluing together sides of the rectangle, our lattice universe map comes from gluing together sides of such a fundamental domain in a particular way.

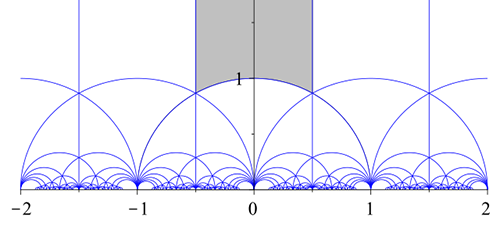
This upper half plane divided up into regions. (It's a tiling of the upper half plane by fundamental domains of the modular group.) Figure kilom691, CC BY-SA 4.0.

The regions don't all look the same to us, but they are related mathematically. In our torus example, each rectangle could be reached from the original one by a translation, that is by shifting the original rectangle in a particular direction by a particular distance. In the case of lattices, the fundamental domains are related by functions called Möbius transformations.

Although the regions all look different to our eyes, the link via Möbius transformation means we know exactly how all the regions are related and we can treat them as one and the same. (Actually, the regions are all the same size if we measure size using something called the hyperbolic metric - but that's something to be explored another time.)

Each region, with sides glued together in a particular way, gives a picture of the universe of lattices. Technically the map is the quotient of the upper half plane by a group of Möbius transformations called the modular group. Similarly to what we said above, the quotient comes from stacking all the regions back on top of each other with the help of the Möbius transformations that relate them, merging the stack down, and then gluing the sides in a way given by two particular Möbius transformations that can be used to generate the whole group.

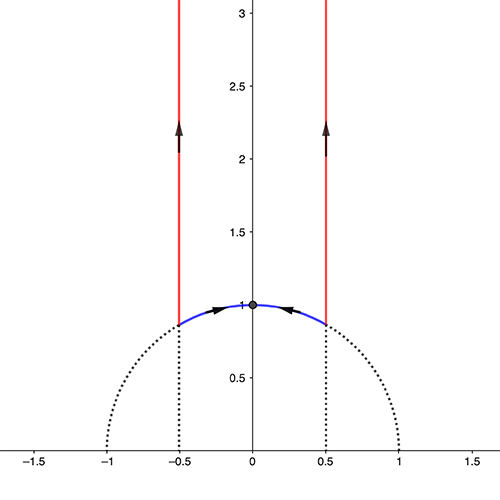
The region with red and blue sides is a fundamental domain. The moduli space of Riemann tori is what you get when you glue the two red sides and the two blue sides so that the directions of the arrows match up. The moduli space is itself a surface.

Since each Riemann torus is linked to a lattice, the map of all lattices now gives us the moduli space of Riemann tori, which we were after. Moving around this moduli space we can visit each Riemann torus that exists (considering those that are isomorphic as being the same). Paying attention to how the parallelograms defining the lattices change as we move around moduli space allows mathematicians to see how the notion of angle changes in the Riemann tori we visit as we move along our path. They can also get a sense of how far apart (i.e. how similar) two given Riemann tori are and of how big the world of Riemann tori is compared to, say, the world of all Riemann surfaces with two holes.

More generally, having found the moduli space of Riemann tori, mathematicians can say they have understood the entire universe of these surfaces and how they all fit together.

Equations anyone?

If you haven't had enough yet, there's another fascinating twist to the story. It turns out that a Riemann torus can also be related to the set of all (complex number) solutions x and y to an equation of the form

$$y^3=x^3+ax+b,$$ where $a$ and $b$ are complex numbers.

Such sets of solutions are also known as elliptic curves and they belong to the more general family of algebraic varieties, which we looked at in this article.

This means that you can find yourself in the land of surfaces even if you're not originally interested in geometry or topology at all, but in equations and their solutions, that is, in number theory. For an example of this, read our article on the work of the mathematician Manjul Bhargava. Elliptic curves also play an important role in Andrew Wiles' proof of Fermat's famous last theorem — find out more here.

The link to equations is also useful when it comes to looking for moduli spaces of Riemann surfaces with more than one hole. In this case, it's no longer possible to use lattices to understand what's going on. But because such surfaces can also be described in terms of equations, mathematicians branch out into the world of algebraic geometry, harnessing the power of algebra to understand the shapes they are interested in.

The research programme at the INI which inspired this article involved constructing moduli spaces for higher-dimensional shapes (rather than just surfaces, which have two dimensions) and developing techniques for understanding their geometry. Exciting new tools have been developed in this area over the last 15 years or so, and the mathematicians taking part in the programme have been leveraging this new technology.

The understanding of moduli spaces feeds back into our understanding of the individual shapes that make them up — very often geometric questions about these shapes become questions about the moduli spaces they belong to. Moduli spaces also play an important role in enumerative geometry, which is about counting objects (such as curves) of a particular type. Amazingly, the results mathematicians have come up with are also relevant to string theory, physicists' attempt to describe all the goings-on in our Universe in terms of a single unifying mathematical framework.

This is why the INI research programme brings together leading experts from different areas of maths, all attacking the problems to be solvedfrom their particular point of view. It's this combining of forces that often leads to great progress in maths.

About this article

Ruadhaí Dervan (second from left) and Victoria Hoskins (third from left) together with two other organisers of the research programme, Frances Kirwan (left) and Gergely Berczi (right).

This article was inspired by the research programme New equivariant methods in algebraic and differential geometry which took place at the Isaac Newton Institute for Mathematical Sciences in Cambridge between January and June 2024. It was produced in collaboration with Ruadhaí Dervan and Victoria Hoskins, who co-organised the programme.

Ruadhaí Dervan is a Senior Lecturer at the University of Glasgow, where he researches the geometry of higher-dimensional spaces.

Victoria Hoskins is an assistant professor at Radboud University Nijmegen, where she researches symmetries and moduli spaces in algebraic geometry.

Marianne Freiberger is Editor of Plus and would like to thank Ruadhaí and Victoria for all their help with this article.

This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI). The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. The Newton Gateway is the impact initiative of the INI, which engages with users of mathematics. You can find all the content from the collaboration here.