
The murmuration conjecture: finding new maths with AI
Artificial intelligence (AI) is changing our lives. Many of us use the voice activated features on our phones to recognise, understand and fairly complex speech. Students use ChatGPT to do their homework. And doctors use AI algorithms to help diagnose many diseases from medical data.
Yang-Hui He, a professor at the London Institute of Mathematical Sciences, became interested in artificial intelligence in 2017, partly out of intellectual curiosity, but also because of a change in personal circumstance. "I remember well as that was when my son was born!" says He. "I had infinite time at 3am having been woken up to feed him and thought – let's do something crazy!"
At the time AI was already revolutionising many areas of science that were impacting our lives, such as improving blood tests and cancer screening, and supporting conservation and improving traffic. As a mathematician, He was interested in whether AI could be turned to more theoretical uses.
He began his research career studying the interface between mathematical physics, string theory and algebraic geometry. One class of the mathematical objects that lives at this interface are Calibi-Yau manifolds. As we saw in our previous discussion with He, these fascinating geometric structures provide a way to hide the extra, tightly curled dimensions that string theory requires. (You can find out more in our article Hidden dimensions.) And so mathematicians and physicists were very interested in understanding these manifolds, and in particular, classifying them into different types. But this turned out to be very difficult, so He's idea was to use AI to help.
Machine learning
Machine learning is the most significant recent development in artificial intelligence. If you have a task you want to perform – say you want to classify a bunch of images into whether they are pictures of cats, or pictures of dogs – then rather than explicitly tell computer how to do the task you have it learn how to do the task itself, perhaps by spotting patterns in existing data.
Suppose you have a big set of images with some of them already labelled correctly as cats or dogs. A machine learning algorithm can learn from this set of labelled images how to classify images, and then apply what it has learnt to correctly label images it has never seen before. (You can read more about machine learning in our article What is machine learning?)
Machine learning requires data, and when He had the idea of using machine learning to help understand Calabi-Yau manifolds he knew where to find the data. Mathematicians and physicists had built many databases of Calabi-Yau manifolds, some with millions of examples. Some of the examples were known to have particular important properties, but explicitly checking individual examples to see if they do would require a lot of computing power. Yang designed a machine learning algorithm to try to spot patterns in the databases to see which ones had important properties, and to classify the manifolds accordingly. In this way the algorithm could learn the landscape of these mathematical objects that were key to string theory.
The result was He's paper – Deep learning the landscape of string theory – one of the first papers applying machine learning to theoretical science. It coincided with the work of several independent groups that also had similar ideas of applying machine learning to string theory.
"This was so cool!" says He. "I started making friends with everybody, saying – give me your favourite problem in your branch of mathematics." Machine learning is very good at spotting structures and patterns in data. So if a mathematician had a collection of mathematical objects, He could design a machine learning algorithm to learn shared structures or spot patterns within these collections. "It worked in almost all of the cases!"; (You can find out more in He's text book, The Calabi-Yau Landscape, and the recent book He edited, On machine-learning for pure mathematics and theoretical physics.)
The algorithms could spot these patterns and structures, but there was a problem – the algorithms did not provide any new insights into the mathematics. It took He another five years or so to find a new, more sophisticated approach to creating new mathematics. "Now I'm a little more sophisticated," He says. "I'm trying to understand whether machine learning algorithms can actually assist us in making concrete conjectures."
Elliptic curves
He and his colleagues were interested in something called elliptic curves, which have proved to be incredibly important in number theory. For example when Andrew Wiles famously proved Fermat's last theorem, he actually proved a broader result about elliptic curves. And elliptic curves now play an important role in modern cryptography.
Elliptic curves are defined by simple equations of the form: $$ y^2 = x^3 + ax + b $$ where $a$ and $b$ are some constants. Below are just a few examples of elliptic curves for different values of $a$ and $b$ – the curves show all the real values of $x$ and $y$ that satisfy the equation. (The constants $a$ and $b$ have to satisfy a few basic conditions so that the curve doesn't have any problematic singular points – you can see an example below. You can read more about elliptic curves in the article Answers on a donut.)
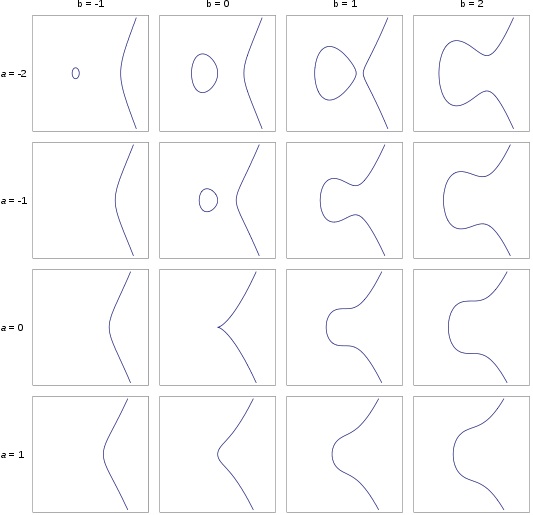
Elliptic curves corresponding to different whole number values of a between -2 and 1 and b between -1 and 2. Note that the curve for a = b = 0 doesn't qualify as an elliptic curve because it has cusp – known as a singular point.
As you can see you get quite different elliptic curves as you vary the values of $a$ and $b$. In fact number theorists have built up databases containing millions of examples of elliptic curves. One thing they are very interested in is the rank of an elliptic curve, which tells us a great deal about the rational solutions of the curve (ie, those $x$ and $y$ that satisfy the elliptic curve equation, where $x$ and $y$ can be expressed as fractions.) For example, if the rank is 0 we know there are only finitely many rational solutions to an elliptic curve. If the rank is 1 we know that the curve has infinitely many rational solutions, and these solutions can be thought of as equivalent to the integers.
Unfortunately calculating the rank of elliptic curves is tricky. It's even the subject of one of the unsolved Millennium prize problems – the Birch Swinnerton-Dyer conjecture (or BSD conjecture for short) named after the mathematicians Brian Birch and Peter Swinnerton-Dyer. You can win one million dollars if you can prove the BSD conjecture is true! (You can read more about the rank of elliptic curves and the BSD conjecture in Answers on a donut.)
Together with his colleagues Tom Oliver, Kyu-Huwan Lee and Alexey Podznyakov, He used databases containing millions of elliptic curves that had been set up by number theorists to study the BSD conjecture. They applied a number of different types of machine learning algorithms to this data to try to predict the rank of the elliptic curves.
Getting a clearer view
All the algorithms did a good job at predicting the rank of the elliptic curves. For He this wasn't very surprising: "In maths there are no accidents. This is very structured data." But what He and his colleagues were particularly interested in was to understand why the machine learning algorithms were working so well. This interpretability of an algorithm – the ability of a human to understand why an algorithm is working – is highly desired in machine learning.
"We tried various machine learning algorithms," says He. "But principal component analysis – the simplest [type of] machine learning ever –that was the key to it." Principal component analysis (PCA) is a way of viewing data in a new, simpler way. It takes data that depends on a lot of variables (high-dimensional data) and projects it into a much lower-dimensional space. In this case it took the elliptic curves in He's databases, which were represented as points in 1000-dimensional space, and rewrote them as points in two dimensions that could be plotted on a page.

Principal component analysis allows the elliptic curves to be plotted in two dimensions, showing the 36,000 randomly chosen elliptic curves clustering into those of rank 0 (blue), rank 1 (red) and rank 2 (green). (Figure from "Murmurations of Elliptic Curves" by Yang-Hui He, Kyu-Hwan Lee, Thomas Oliver and Alexey Pozdnyakov.)
Not only did PCA give He and his colleagues a clearer view of the elliptic curves, this simplest of machine learning techniques also revealed how the algorithm created this clearer view of the data: by taking a very unusual type of average. When Podznyakov, who was an undergraduate intern of Lee at the time, began experimenting with this new way of looking at the data, he saw a very surprising shape emerge.
Murmurations in the prime numbers
"When we first saw the plot of this average my collaborators said it looks like the stuff that birds do – the murmurations of starlings," says He. "And I said - let's call it that! And we got away with it!"
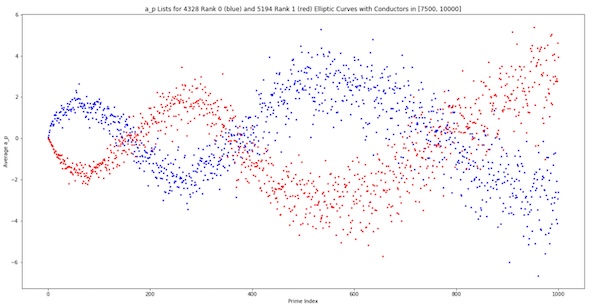
A murmuration of elliptic curves: a plot of this unusual type of average for different randomly chosen elliptic curves. The red dots represent curves of rank 1, the blue curves of rank 0. (Figure from "Murmurations of Elliptic Curves" by Yang-Hui He, Kyu-Hwan Lee, Thomas Oliver and Alexey Pozdnyakov.)
The strange average is calculated for different prime numbers that are associated with the elliptic curves. And when the result is plotted the elliptic curves of different ranks show up as murmurations flowing across the page. "At the beginning we thought this might be trivial," says He. But when the researchers showed their results to experts in number theory they discovered that no one had ever taken this type of average before, and no one had seen this pattern. "They said Birch could have done this, but he didn't take this type of average. Because why would you? It's such a strange thing to do!"
The discovery of these murmurations by He and his colleagues has caused a flurry of work. (You can read more in this recent article in Quanta.)"People are still working on it, it's been over a year now," says He. Number theorists are now hard at work trying to discover new murmurations and learn more. "It's expected to be a general phenomenon in number theory - a fundamental pattern in the prime numbers that somehow has been missed for hundreds of years."
The Birch test – a new test of AI
The discovery of these murmurations of elliptic curves would not have been possible without He and his colleagues first doing the machine learning experiments. He had definitely succeeded in using artificial intelligence to learn new insights into mathematics.
He and his colleagues presented their work on the murmuration conjecture at a research programme at the Isaac Newton Institute for Mathematical Sciences in Cambridge that He helped organise. The programme – Black holes: bridges between number theory and holographic quantum information (BLH) – brought together a fascinating array of experts in black holes, quantum theory, mathematicians and computer scientists. And discussions about their work during the programme helped develop a brand new test of artificial intelligence: the Birch test.
A commonly accepted test for artificial intelligence is the Turing test, devised in 1950 by Alan Turing. In the test a human doesn't know if what they are interacting with via their computer is another human, or an AI algorithm. If the human can't distinguish which is which, the AI is said to have passed the Turing test. The past few years have seen enormous progress in artificial intelligence – anyone who has tried out ChatGPT will understand that it can pass the Turing test already, although only on certain specific tasks.
He and his fellow participants at the BLH programme were interested in a mathematical analogue of the Turing test – that would test if an AI had made a good mathematical discovery. The test is passed if the discovery meets three criteria.
The first criterion is that the result must be entirely generated by AI. The second criterion is that the result must be interpretable: "It must give a theoretic statement that scientists can work on," says He. If you remove the result from the AI framework, there must be a precise statement for someone to prove. And finally, the third criterion is that the result must be non-trivial. It must result in a theoretical insight that will inspire more work in the area.
"So the murmuration conjecture is one of the few that has almost passed this test," says He. "It passes the second and third criteria, but not the first, as we were involved in interpreting the results." Other results, such as one recently produced by Google's DeepMind, passed the first two criteria, but not the third: "it wasn't nontrivial enough and could be proved in a couple of months." So far not a single AI discovery in mathematics has passed the Birch test. "It's very stringent – Birch has very high standards!"
Hedgehogs and birds
The BLH programme offered the opportunity for conversations between experts from many different fields – from physics, string theory, number theory and AI. He says it was conversations like these, as well as the time and space such a research programme provides, that can be so stimulating in producing new ideas such as the Birch test.
"You're never bored! You always get fresh new ideas that you never thought about." says He. The exposure to people in different areas and new ideas fits his personality well, says He. Some people prefer to dive deep into a subject and work on one thing, but not He. "People say there are hedgehogs and birds. Hedgehogs like to burrow deep, and birds like to [look at everything]. We need both types of theorists. I'm definitely not a hedgehog, I like to see the connections."
About this article
Yang-Hui He is a Fellow and professor at the London Institute for Mathematical Sciences. He works on the interface between string theory, algebraic geometry, and machine learning.
Rachel Thomas is Editor of Plus.
This content was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
