
From rainbows to rogue waves
If you've ever marvelled at a rainbow, you have witnessed dispersion in action. Dispersion is where the speed at which a wave moves depends on its frequency, and so wavelength. (You can read a basic introduction to waves and their frequency and wavelengths in Why sine (and cosine) make waves and Give us a wave.)
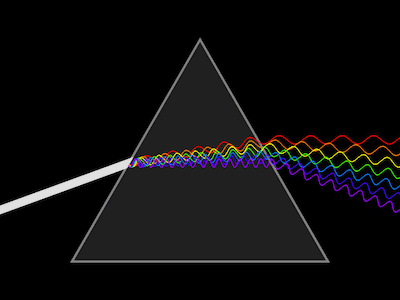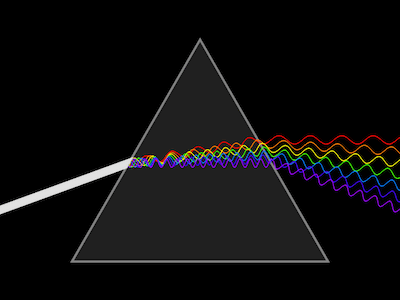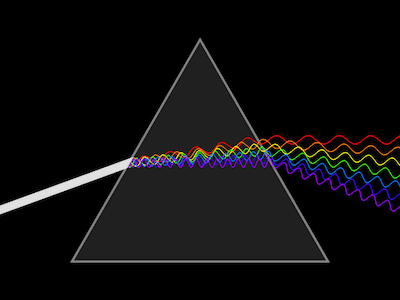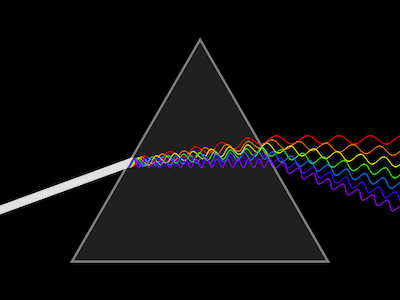
An illustration of the different wavelengths that make up white light being dispersed by a prism. (Image by Lucas Vieira - in public domain)
Rainbows
The most familiar example is the refraction of the different colours that make up white light as they pass through a glass prism or are reflected within droplets of water to make rainbows. When light from the Sun travels through a vacuum (and to a very good approximation through air) all frequencies travel at the same speed, c, roughly 300,000 km per second. However, the speed of the light within water or the glass prism depends on the frequency (and hence colour) of the light. There is only a very small difference in the speed of the different colours of light in water, but this small amount of dispersion is enough to split sunlight into the beautiful spectrum of colours we see in a rainbow. (You can read more in our article Maths behind the rainbow and in our introduction to dispersion Maths in a minute: Dispersion.)
The mathematics that describes dispersion is complex and a very active area of research. It is also an area with a large number of applications, including applications in fluid dynamics, explained Mark Hoefer, one of the organisers of a six month research programme running at the Isaac Newton Institute (INI). "People are doing new experiments in water waves, with new observations and questions about understanding them and bringing these techniques to bear," says Hoefer. Another big area is nonlinear optics which has applications in improving lasers, communications and information processing.
"Our program is quite remarkable in that it's very broad and quite interdisciplinary in nature," says Barbara Prinar, another organiser of the programme. "The program will bring together people from different communities that don't normally have a chance of talking and collaborating over a relatively extended period of time. So we definitely anticipate a lot of cross-pollination between fields."
A good example of this is the recent event From Dispersive Hydrodynamics to Forecasting, Machine Learning and Back. Organised by the Newton Gateway to Mathematics, this Open For Business event aims to bring people working on applications outside of mathematics together with the researchers involved in an INI programme. The event directly followed and built on a scientific workshop, and brought together meteorologists and climate modellers to focus on applications of this area of mathematics to weather and climate forecasting and to oceanography.
Rogue waves
"Waves in nature are not necessarily simple," said Gennady El, another organiser of the programme, in their introduction to the Open For Business event. "We need new methods to predict real wave phenomena, such as rogue waves."
Rogue waves are giant single waves with significant power for destruction. They exist only fleetingly – seeming to appear from nowhere and quickly disappear. "Most of the time we have no evidence of [rogue] waves at all," said one of the speakers, Peter Janssen, from the European Centre for Medium-Range Weather Forecasts. "It's a very fickle event." They last only for seconds to a few minutes at most, giving a very short time in which to capture data and that data will be limited. "The challenge is to say something about the occurrence of these events."
Although sailors had reported them for centuries, rogue waves were only scientifically recorded for the first time in 1995. The Draupner oil rig was built to withstand 20 metre waves, which were only predicted to occur once in 10,000 years. But in 1995, the rig was swamped by a single 26 metre high wave. Sensors in the rig's platform and base captured this fleeting phenomenon, finally confirming the existence of rogue waves.
The Drampner wave data, and other real world data gathered since, led oceanographers to rethink their mathematical models and they now believe rogue waves are common. Around ten rogue waves are thought to be arising in oceans around the world at any one moment and they are now thought to be responsible for the sinking of many ships in past and recent history.
There are many competing mathematical theories to describe how rogue waves might occur. The basic idea is that different surface ocean waves interact in such a way that their peaks coincide and reinforce each other to produce steeper waves, said Janssen. "There are a number of nonlinear processes that cause this focussing of the wave energy." Such nonlinear effects can result from specific dispersion conditions, allowing a wave to temporarily borrow energy from its neighbours. This new theoretical understanding has led to new laboratory experiments which have reproduced the rogue wave phenomena observed on the ocean.

Images from the 2019 simulation of the Draupner wave show how the steepness of the wave forms. (Image: McAllister et al 2019 – CC BY 4.0)
Dispersive hydrodynamics is key to understanding such complex behaviour seen in oceanography, and other phenomena in weather and climate modelling. All of these areas also come with vast amounts of data, making them obvious opportunities to apply a form of artificial intelligence called machine learning. "Machine learning is helping more and more to inform the modelling, and techniques from nonlinear mathematics are being used to understand fundamental behaviour of neural networks and the algorithms based on these," says Antonio Moro, one of the organisers of the programme. "New research is developing both in the theory and the applications."
New mathematics, new experiments, new researchers
This cross-pollination is one of the main opportunities of the INI programme, with collaborations between pure and applied mathematicians and experimental physicists , says El. "New mathematical results suggest new physical experiments. And this is what's actually happening during this programme – new collaborations are already being established here."
Hydrodynamic dispersion is a relatively new field, and a key aspect of the programme is also to encourage and support early career researchers to advance the field. "There are interactions between up-and-coming stars in the field, they're talking to each other and they're also talking to senior people," says Shearer. "This is a field that in a way is in its infancy but there's a lot of excitement about it, and so it's great to be able to sort of inspire the [next] generation and they will take over to carry the subject forward."
About this article
This article was produced as part of our coverage of the Dispersive hydrodynamics: mathematics, simulation and experiments, with applications in nonlinear waves programme hosted by the Isaac Newton Institute for Mathematical Sciences. You can find more content about the programme here.
This article is based in part on an interview by the INI's Dan Aspel with organisers Antonio Moro, Michael Shearer, Mark Hoefer, Gennady El, and Barbara Prinari, and on the first Open For Business event of the programme, held on 24 October 2022 and organised by the Newton Gateway to Mathematics.
Rachel Thomas is Editor of Plus.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
