Article


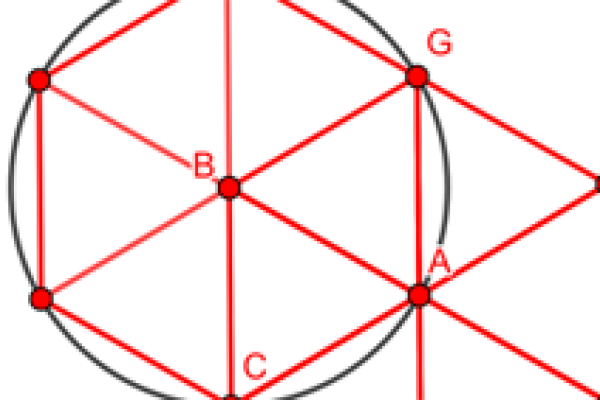
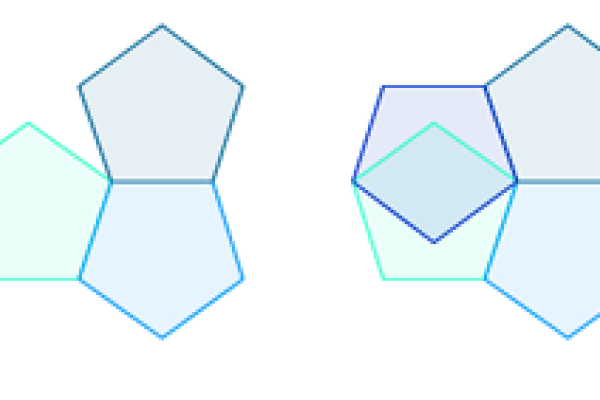
A tip of the hat: Celebrating an aperiodic monotile
Here's a look at the shape that can tile the plane in a non-repetitive pattern — and some of the creative uses people have found for it.