This article describes how you can describe the entire universe of Riemann tori (surfaces that look like dooughnuts) in one go.
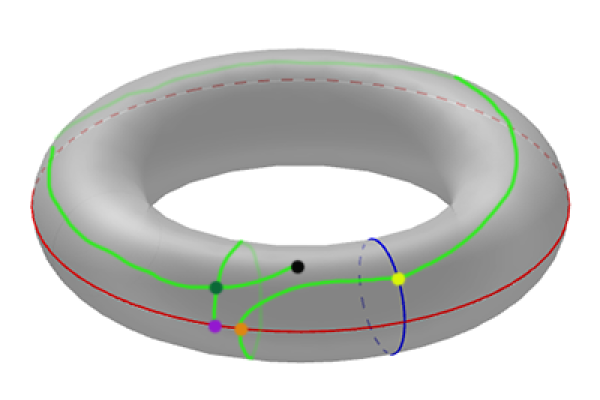
A Riemann torus is a surface that looks like a doughnut. This articles explored how you might tell Riemann tori apart.
How many different surfaces are there? The question seems impossible to answer, but mathematicians have a way of dealing with the multitude. Follow us on a journey into the world of moduli spaces.
How many different surfaces are there? The question seems impossible to answer but mathematicians are good at dealing with multitudes. Follow us into the world of moduli spaces!
From tiling bathrooms to fooling cancer cells, and from new insights in topology to bringing research into the classroom — we hope you enjoy our April round-up!
Our neighbour Oscar Randal-Williams tells us about his exciting work at the frontiers of mathematics and the fundamental question he might be just about to answer!
We guide you through an exciting recent breakthrough in the world of topology, involving something called the telescope conjecture.
The concept of homotopy is a great example of how the language of maths can make intuition precise.
Barry Mazur has received the 2022 Chern Medal for profound discoveries in topology, arithmetic geometry and number theory.
