Living through the flu season can feel like living through a lottery. You know that lots of people have it, but whether you catch it is pot luck.

Despite this randomness, most of us are aware that epidemics aren't entirely unpredictable. Epidemiologists use mathematics to get a sense of how a particular epidemic might play out. We saw this during the COVID-19 pandemic when mathematical models took centre stage.

The reason this is possible is that, once enough people are infected, variability between people cancels out. For every highly sociable superspreader there's a hermit who infects no one else (loosely speaking). In this situation assuming that every infection generates the same average number R of new cases can get us a long way in making predictions. It's the same reason why population statistics have predictive power. We can't say how many children an individual is going to have in their lifetime, but cancelation of variability means that we can work with averages when having a stab at predicting whether a population will grow or decline.

A very different situation occurs, however, when a new infectious disease has just entered a population and not many people have caught it yet. Imagine an infected traveller entering a country. If the traveller is alone in their car, goes straight home and stays there until they recover, the disease may never spread. If they arrive on a crowded train and go to a party, they may seed a large wave of infections. In the early stage of an outbreak variations between people don't cancel out and everything depends on who catches the disease and when — this can make the difference between a public health nuisance and a large-scale outbreak. If there's a lot of variability in the population then the randomness (also called stochasticity) is more pronounced.

This stochasticity can be deceiving. "You can have [outbreaks] that take off very quickly, but you can also have [outbreaks] that stutter along until they take off much later," says Jacob Curran-Sebastian, a postdoctoral researcher at the Department of Public Health at the University of Copenhagen, who works on stochastic modelling. "[It's all] down to the randomness of who gets infected when and who is transmitting the most. The same is true for extinction. There's lots of variability in how long it takes an outbreak to go extinct."

It's a bit like gambling. A lucky streak at the start of your night doesn't mean you'll go home rich and an unlucky one doesn't mean you'll end up broke.

Real life randomness

There are many examples of stochasticity making it hard to predict the scale of an outbreak early on. Deirdre Hollingsworth, Professor of Infectious Disease Epidemiology at the Centre for Global Health Research at the University of Oxford, points to the early days of HIV which, genetic analysis suggests, had been circulating from the 1920s before it was identified as an unknown syndrome in the 1980s. "[It's thought] that this was because [initially the virus circulated] in isolated populations that were not very well connected," she says.

Something similar was probably the case for the Ebola outbreak in West Africa from 2014 to 2016. "The virus emerged in a village where Ebola had not previously been seen, but was detected when it had spread to major cities. An unfortunate series of chance events led to it being such a disastrous outbreak "

At the time of writing of this article a viral disease called mpox is also presenting a stochastic puzzle. Since autumn 2023 Central Africa, in particular the Democratic Republic of the Congo (DRC), has seen what you might describe as a steady drip of cases, ending in what appears to be a surge. This follows the discovery of a new genetic type of the mpox virus, called clade Ib. The slow start confronted health officials in the UK with the difficult choice of whether or not to invest in expensive vaccine doses that would be used should the outbreak spill over to the UK. "There were people saying it's not going to become an epidemic. But just because a disease has been circulating for months and hasn't emerged as a large epidemic, doesn't mean it's not going to," says Hollingsworth.

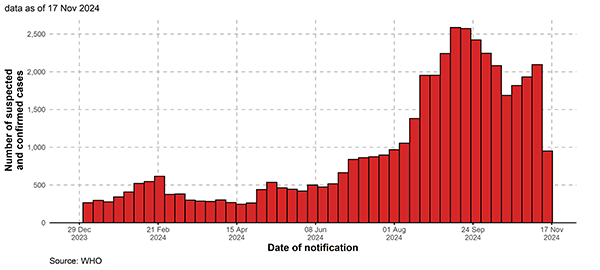
All cases of mpox, including suspected and lab confirmed cases, in the Democratic Republic of the Congo shown from 2024. From 2022-24 Mpox Outbreak: Global Trends. Geneva: World Health Organization, 2024 (last cited: 22/22/2024).

After the World Health Organization declared the DRC outbreak a public health emergency of international concern in August 2024, the UK did order 150,00 vaccine doses. And indeed — clade Ib cases have been detected in the UK, in a returning traveller and three of their close contacts. Further contacts of the infected people are being followed up and offered testing and vaccination. In the absence of such measures (and to some extent even with these measures in place) whether the outbreak in the UK grows to beyond a handful of cases would depend on the luck of a draw.

Quantifying chance

All this doesn't mean that mathematics can tell us nothing at all in the early stages of an outbreak. It is possible, for example, to simulate the stochastic nature of an outbreak using a hypothetical population and a metaphorical roll of a die (see here for a very simple example). Running lots and lots of such simulations on a computer you get an idea of the landscape of all the possible courses an outbreak can take. If a large epidemic results in a large proportion of the simulations, then you might conclude that a large outbreak is likely in real life too. If the outbreak dies out in most of the simulations, then you might feel safer.

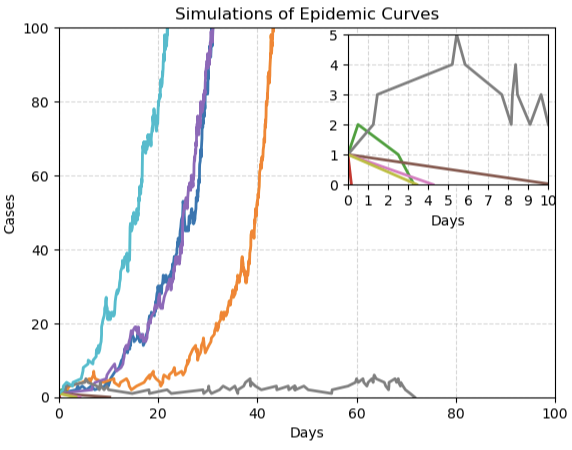
This figure shows ten simulated epidemic curves. Four of them (cian, purple, blue and orange) start on their exponential trajectory at different times. Five of them go extinct straight away (to see these better, see the magnified box at the top right). The remaining curve (grey) keeps going for about 70 days before extinction. Figure by Jacob Curran-Sebastian, made using stochastic modelling.

Using this general idea (and a lot of much more sophisticated mathematics than we described here) it's possible to quantify the uncertainty you're faced with in a particular situation. This is called stochastic modelling. "For certain models you can calculate the probability that, under this model, the outbreak will go extinct or, conversely, that it will take off," says Curran-Sebastian. The approach can help with contingency planning.

What we can't get away from, however, is that all we can come up with are probabilities, not certainty. Understanding all the possible trajectories an outbreak can take, doesn't tell you which trajectory you happen to be on right now.

Again, gambling gives a good analogy. Rolling a die many times gives you a good idea of whether the die is fair or loaded, so you can estimate the chance that betting on a particular number will win you money. That's useful information if you're planning to bet on many rolls. If you only have one roll, however, the abstract concept of a probability isn't so meaningful. Any outcome is still possible.

About this article

Jacob Curran-Sebastian is a postdoctoral researcher based at the University of Copenhagen. His research is on stochastic models of epidemics with a particular focus on modelling uncertainty in the early phase of disease outbreaks.

Deirdre Hollingsworth is Professor of Infectious Disease Epidemiology at the Centre for Global Health Research at the University of Oxford.

Marianne Freiberger, Editor of Plus, interviewed Curran-Sebastian and Hollingsworth in October 2024.

This article is part of our collaboration with JUNIPER, the Joint UNIversities Pandemic and Epidemiological Research network. JUNIPER is a collaborative network of researchers from across the UK who work at the interface between mathematical modelling, infectious disease control and public health policy. You can see more content produced with JUNIPER here.