
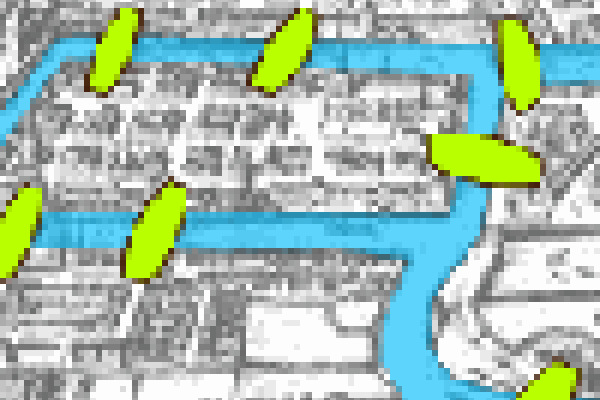
The bridges of Königsberg
Can you find a path through on this city map that crosses every bridge exactly once? Euler's answer to this problem started off the filed of graph theory.

Can you find a path through on this city map that crosses every bridge exactly once? Euler's answer to this problem started off the filed of graph theory.


Sometimes a piece of maths can be so neat and elegant, it makes you want to shout "eureka!" even if you haven't produced it yourself. One of our favourite examples is the art gallery problem.
Mathematicians and psychologists don't cross paths that often and when they do you wouldn't expect it to involve an (apparently) unassuming puzzle like the Tower of Hanoi. Yet, the puzzle holds fascination in both fields.
In the 1930s the logician Kurt Gödel showed that if you set out proper rules for mathematics, you lose the ability to decide whether certain statements are true or false. This is rather shocking and you may wonder why Gödel's result hasn't wiped out mathematics once and for all. The answer is that, initially at least, the unprovable statements logicians came up with were quite contrived. But are they about to enter mainstream mathematics?