
Teacher package: Rational and irrational numbers
The Plus teacher packages are designed to give teachers (and students) easy access to Plus content on a particular subject area. Most Plus articles go far beyond the explicit maths taught at school, while still being accessible to someone doing GCSE and A level maths. They put classroom maths in context by explaining the bigger picture — they explore applications in the real world, find maths in unusual places, and delve into mathematical history and philosophy. We therefore hope that our teacher packages provide an ideal resource for students working on projects and teachers wanting to offer their students a deeper insight into the world of maths.
Rational and irrational numbers

Articles in this section are divided into three categories: the first only looks at the rational numbers and the fun that can be had with them, the second explores the irrational numbers and how they interact with the rest of the number line, and the third and fourth take a look at our favourite irrational numbers: the golden ratio and pi.
Don't forget about our sister site NRICH, which has hands-on problems, activities and articles on rational and irrational numbers.
Rational numbers

Having fun with unit fractions — The number 1 can be written as a sum of unit fractions, that is fractions with 1 in the numerator. But how long can we make such a sum?
The magical mathematics of music — Why do some notes go better together than others? It's thanks to fractions!
Music and Euclid's algorithm — What does a mathematician from the 3rd century BC have to do with tuning musical instruments in 17th century Europe? This is article describes how musical pitch translates into ratios between whole numbers.
A glimpse of Cantor's paradise — Between any two whole numbers there are infinitely many rational numbers. So does that mean that there are "more" rationals than whole numbers? It doesn't and this article tells you how to prove it.
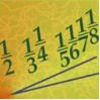
In perfect harmony — Adding up fractions is one of the first really tricky thing we come across at school. But what if you add up infinitely many of them? This article takes a good look at the harmonic series.

Outer space: The rule of two — Another look at an infinite series of fractions with a nice geometrical representation of the answer.
Outer space: Is this a record? — The harmonic series revisited, this time to understand sporting records.
Irrational numbers
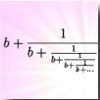
Chaos in numberland: the secret life of continued fractions — One of the most striking and powerful means of presenting numbers is completely ignored in the mathematics that is taught in schools, and it rarely makes an appearance in university courses. Yet the continued fraction is one of the most revealing representations of many numbers, endowing even unwieldy irrationals with extraordinary patterns and symmetries.
Some benefits of irrationality — How irrational numbers can help you beat that photocopier.

Transcendental meditation — Here's the famous proof of the irrationality of the square root of 2 and a look at algebraic and transcendental numbers.

Dynamic numbers: the work of Elon Lindenstrauss — One of the 2010 Fields Medals — the highest honour in mathematics — was awarded to Elon Lindenstrauss for work inspired by the simple problem of how to approximate irrational numbers by rational ones.
A tale of two curricula: Euler's algebra textbook — Leonhard Euler was one of the most prolific mathematicians of all times. This article looks at his famous textbook, Elements of algebra, including a discussion of irrational numbers in Euler's own words.
The golden ratio
The golden ratio and aesthetics — It was Euclid who first defined the golden ratio, and ever since people have been fascinated by its extraordinary properties. Find out if beauty is in the eye of the beholder, and how the golden ratio crosses from mathematics to the arts.
Decoding Da Vinci: Finance, functions and art — Dan Brown in his book, The Da Vinci Code, talks about the golden ratio as having a "fundamental role in nature". Brown's ideas are not completely without foundation, as the proportion crops up in the mathematics used to describe the formation of natural structures like snail's shells and plants, and even in Alan Turing's work on animal coats. But Dan Brown does not talk about mathematics, he talks about a number. What is so special about this number?

The life and numbers of Fibonacci — Another look at the golden ratio as the limit of the Fibonacci sequence.
Maths and art: the whistlestop tour — Our brains have evolved to take pleasure in rhythm, structure and pattern. Since these topics are fundamentally mathematical, it should be no surprise that mathematical methods can illuminate our aesthetic sense. And the golden ratio plays an important role in this.
Pi
What is the area of a circle? — You might know the famous formula for an area of a circle, but why does this formula work? This explanation really is a piece of cake, served up with a hefty estimate of pi.

Pi not a piece of cake — The decimal expansion of pi is infinitely long and there are no obvious patterns in it. But are the digits truly random? This story describes how a new formula for pi got us a little closer to an answer.
Number crunching ants — What does a bread-throwing Frenchman have in common with a tiny species of ant with a brain smaller than a single grain of salt? It's a serious question and the intriguing answer has taken scientists and mathematicians years to find — and it involves our favourite number pi.
Computer geeks break pi record — This story describes how two computer geeks calculated pi to 5 trillion places, on a single desktop and in record time.